
 ,
,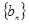 满足:
满足: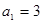 ,当
,当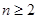 时,
时,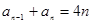 ;对于任意的正整数
;对于任意的正整数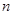 ,
,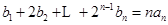 .设
.设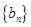 的前
的前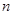 项和为
项和为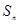 .
.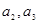 ,并求数列
,并求数列 的通项公式;
的通项公式;
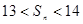 的
的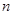 的集合.
的集合.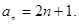 (2)
(2)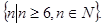
 的通项公式是求解本题的关键.由
的通项公式是求解本题的关键.由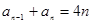 及
及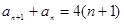 两式相减可得:
两式相减可得: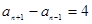 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为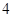 ,而
,而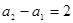 ,故
,故 是公差为
是公差为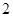 的等差数列.
的等差数列.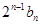 }的通项公式,进而求出
}的通项公式,进而求出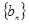 的通项公式.
的通项公式.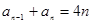 中,取
中,取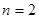 ,得
,得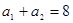 ,又,
,又,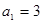 ,故
,故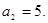 同样取
同样取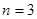 可得
可得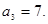 ……………………
…………………… 分
分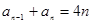 及
及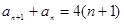 两式相减可得:
两式相减可得: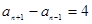 ,所以数列
,所以数列 的奇数项和偶数项各自成等差数列,公差为
的奇数项和偶数项各自成等差数列,公差为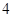 ,而
,而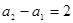 ,故
,故 是公差为
是公差为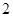 的等差数列,
的等差数列,
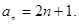 ……………………
…………………… 分
分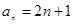 而未能证明的扣
而未能证明的扣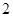 分;用数学归纳法证明不扣分.
分;用数学归纳法证明不扣分.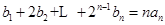 中令
中令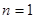 得
得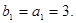 ……………………
……………………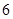 分
分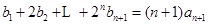 ,与
,与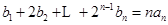 两式相减可得:
两式相减可得: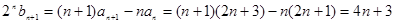 ,
, ,即当
,即当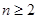 时,
时,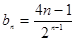
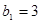 也符合该式,所以,
也符合该式,所以,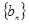 的通项公式为
的通项公式为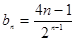 ………………9分
………………9分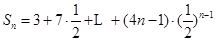 .
.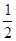
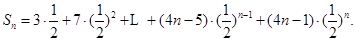
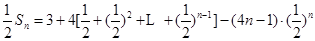
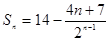 ……………………11分
……………………11分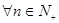 ,
, ……………………12分
……………………12分 ,注意到
,注意到 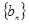 的各项为正,故
的各项为正,故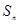 单调递增,所以满足
单调递增,所以满足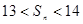 的
的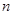 的集合为
的集合为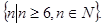 ……………………14分.
……………………14分.

科目:高中数学 来源:不详 题型:单选题
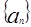 满足
满足 ,则称数列
,则称数列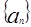 为“等方比数列”甲:数列
为“等方比数列”甲:数列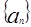 为“等比数列”;乙:数列
为“等比数列”;乙:数列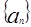 为“等方比数列”;则
为“等方比数列”;则| A.甲是乙的充分不必要条件, |
| B.甲是乙的必要不充分条件, |
| C.甲是乙的充要条件, |
| D.甲既不是乙的充分条件也不是乙的必要条件, |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
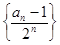 为等差数列;
为等差数列;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com