
| A、8π | B、12π |
| C、16π | D、20π |
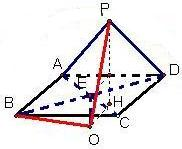 解:设球心为O,如图.
解:设球心为O,如图.| 3 |
| 5 |


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:
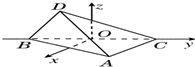 如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标为(
如图,在空间直角坐标系中,BC=2,原点O是BC的中点,点A的坐标为(
| ||
| 2 |
| 1 |
| 2 |
| AD |
| AD |
| BC |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| 4 |
| A、3x+4y-14=0 |
| B、3x-4y+14=0 |
| C、4x+3y-14=0 |
| D、4x-3y+14=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2015届宁夏银川市高三9月月考文科数学试卷(解析版) 题型:选择题
下列四种说法中,错误的个数是( )
①A={0,1}的子集有3个
②“若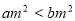 ,则
,则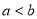 ”的逆命题为真
”的逆命题为真
③“命题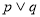 为真”是“命题
为真”是“命题 为真”的必要不充分条件
为真”的必要不充分条件
④命题“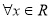 ,均有
,均有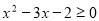 ”的否定是:“
”的否定是:“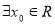 ,使
,使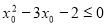 ”
”
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:高中数学 来源:2015届宁夏高三上学期第二次月考试卷文科数学试卷(解析版) 题型:解答题
已知向量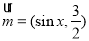 ,
,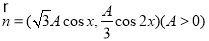 ,函数
,函数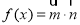 的最大值为6.
的最大值为6.
(1)求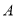 ;
;
(2)将函数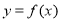 的图象向左平移
的图象向左平移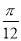 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的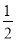 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数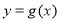 的图象.求
的图象.求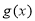 在
在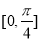 上的值域.
上的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com