
中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五名男记者和编号分别为6,7,8,9的四名女记者.要从这九名记者中一次随机选出两名,每名记者被选到的概率是相等的,用符号(x,y)表示事件“抽到的两名记者的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求所抽取的两名记者的编号之和小于17但不小于11或都是男记者的概率.
解析: (1)共有36个基本事件,列举如下:(1,2),(1,3),(1,4),(1,5),(1,6),(1,7),(1,8),(1,9),(2,3),(2,4),(2,5),(2,6),(2,7),(2,8),(2,9),(3,4),(3,5),(3,6),(3,7),(3,8),(3,9),(4,5),(4,6),(4,7),(4,8),(4,9),(5,6),(5,7),(5,8),(5,9),(6,7),(6,8),(6,9),(7,8),(7,9),(8,9),共36个.
(2)记事件“所抽取的记者的编号之和小于17但不小于11”为事件A,即事件A为“x,y∈{1,2,3,4,5,6,7,8,9},且11≤x+y<17,其中x<y”,由(1)可知事件A共含有15个基本事件,列举如下:(2,9),(3,8),(3,9),(4,7),(4,8),(4,9),(5,6),(5,7),(5,8),(5,9),(6,7),(6,8),(6,9),(7,8),(7,9),共15个.“都是男记者”记作事件B,则事件B为“x<y≤5”,包含:(1,2),(1,3),(1,4),(1,5),(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共10个.故P(A)+P(B)=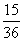 +
+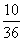 =
=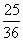 .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
设命题p:关于x的不等式2|x-2|<a的解集为;命题q:函数y=lg(ax2-x+a)的值域是R.如果命题p和q有且仅有一个正确,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
|
| 男 | 女 | 总计 |
| 爱好 | 40 | 20 | 60 |
| 不爱好 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
由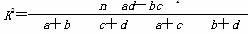 算得,
算得,
K2=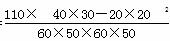 ≈7.8.
≈7.8.
附表:
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.有99%以上的把握认为“爱好该项运动与性别有关”
B.有99%以上的把握认为“爱好该项运动与性别无关”
C.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”
D.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆M: =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}中,a1=1,an+1= (n∈N*).
(n∈N*).
(1)求数列{an}的通项an;
(2)若数列{bn}满足bn=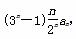 数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
数列{bn}的前n项和为Tn,若不等式(-1)nλ<Tn对一切n∈N*恒成立,求λ的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com