
已知椭圆M: =1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4
=1(a>b>0)的短半轴长b=1,且椭圆上一点与椭圆的两个焦点构成的三角形的周长为6+4 .
.
(1)求椭圆M的方程;
(2)设直线l:x=my+t与椭圆M交于A,B两点,若以AB为直径的圆经过椭圆的右顶点C,求t的值.
解析: (1)由题意,可得2a+2c=6+4 ,即a+c=3+2
,即a+c=3+2 ,
,
因为b=1,所以b2=a2-c2=1,a-c=3-2 ,解得a=3,c=2
,解得a=3,c=2 ,所以椭圆M的方程为
,所以椭圆M的方程为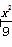 +y2=1.
+y2=1.
(2)由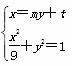 消去x得(m2+9)y2+2mty+t2-9=0.
消去x得(m2+9)y2+2mty+t2-9=0.
设A(x1,y1),B(x2,y2),则y1+y2=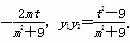 .①
.①
因为以AB为直径的圆过椭圆的右顶点C(3,0),所以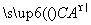 ·
·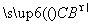 =0.
=0.
由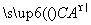 =(x1-3,y1),
=(x1-3,y1),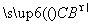 =(x2-3,y2)得(x1-3)(x2-3)+y1y2=0.
=(x2-3,y2)得(x1-3)(x2-3)+y1y2=0.
将x1=my1+t,x2=my2+t代入上式,
得(m2+1)y1y2+m(t-3)(y1+y2)+(t-3)2=0,
将①代入上式,解得t=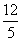 或t=3.
或t=3.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
已知全集U=R,集合M={x|-2≤x-1≤2}和N={x|x=2k-1,k=1,2,…}的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有________个.
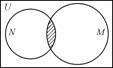
查看答案和解析>>
科目:高中数学 来源: 题型:
中国共产党第十八次全国代表大会期间,某报刊媒体要选择两名记者去进行专题采访,现有记者编号分别为1,2,3,4,5的五名男记者和编号分别为6,7,8,9的四名女记者.要从这九名记者中一次随机选出两名,每名记者被选到的概率是相等的,用符号(x,y)表示事件“抽到的两名记者的编号分别为x、y,且x<y”.
(1)共有多少个基本事件?并列举出来;
(2)求所抽取的两名记者的编号之和小于17但不小于11或都是男记者的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5.若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题.某单位在国家科研部门的支持下,进行技术攻关,采用了新工艺,把二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本y(元)与月处理量x(吨)之间的函数关系可近似地表示为y=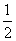 x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M为线段PB的中点.有以下四个命题:
①PA∥平面MOB;②MO∥平面PAC;③OC⊥平面PAC;④平面PAC⊥平面PBC.
其中正确的命题是________(填上所有正确命题的序号).
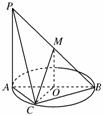
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com