
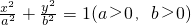 的面积为πab,设平面区域
的面积为πab,设平面区域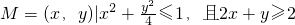 .
.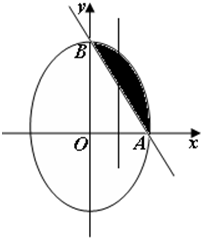 解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的
解:(I)由题意可得:平面区域M如图中阴影部分,则它的面积为此椭圆面积的 再减去△OAB的面积,---(3分)
再减去△OAB的面积,---(3分) 为
为 ,三角形OAB的面积为1,
,三角形OAB的面积为1,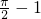 ;---(6分)
;---(6分)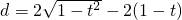 ,---(10分)
,---(10分)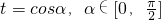 ,
,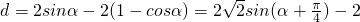
 时,
时,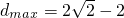 .---(14分)
.---(14分) 再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.
再减去△OAB的面积,结合题中的条件计算出各部分的面积进而达到答案.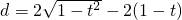 ,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.
,再利用三角换元的有关知识与三角函数的有关性质求出最大值即可.

 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:
| 1 |
| |OA|2 |
| 1 |
| |OB|2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
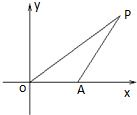 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S,| OA |
| AP |
| OA |
| 3 |
| 4 |
| OP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•安徽)如图,F1、F2分别是椭圆C:
(2012•安徽)如图,F1、F2分别是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2015届福建晋江季延中学高二上学期期中考试文数学试卷(解析版) 题型:解答题
如图,F1,F2分别是椭圆C: +
+ =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°

(1)求椭圆C的离心率;
(2)已知△AF1B的面积为40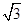 ,求a,b的值
,求a,b的值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com