
分析 (1)利用两个向量的数量积,两角和的正弦公式、诱导公式求得cosB的值,可得B的值.再根据 S△ABC=$\sqrt{3}$,以及余弦定理求得a的值.
(2)利用正弦定理、基本不等式求得ac的最大值,可得△ABC面积为S的最大值.
解答 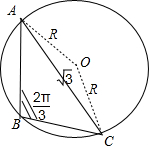 解:(1)△ABC中,∵$\overrightarrow{m}$=(2a+c,b),$\overrightarrow{n}$=(cosB,cosC),
解:(1)△ABC中,∵$\overrightarrow{m}$=(2a+c,b),$\overrightarrow{n}$=(cosB,cosC),
且$\overrightarrow{m}$•$\overrightarrow{n}$=(2a+c)cosB+bcosC=0,
∴再利用正弦定理可得2sinAcosB+sinCcosB+sinBcosC=0,
即2sinAcosB=-sin(B+C)=-sinA,∴cosB=-$\frac{1}{2}$,∴B=$\frac{2π}{3}$.
由正弦定理可得△ABC的外接圆的直径2R=$\frac{b}{sinB}$=$\frac{\sqrt{21}}{\frac{\sqrt{3}}{2}}$.
∵S△ABC=$\frac{1}{2}$ac•sinB=$\frac{1}{2}$ac•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,∴ac=4 ①.
∵b=$\sqrt{21}$,再利用余弦定理可得b2=a2+c2-2ac•cosB=a2+c2+ac=21②,
由①②求得a=4,或a=1.
(2)由(1)可得B=$\frac{2π}{3}$,∵b=$\sqrt{21}$,设△ABC的外接圆的圆心为O,
由余弦定理可得b2=3=a2+c2-2ac•cosB=a2+c2+ac≥3ac,
∴ac≤1,故△ABC面积为 S=$\frac{1}{2}$•ac•sinB≤$\frac{1}{2}$•1•$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{4}$,
故△ABC面积为S的最大值为$\frac{\sqrt{3}}{4}$.
点评 本题主要考查两个向量的数量积,两角和的正弦公式、诱导公式,正弦定理,基本不等式的应用,属于中档题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:解答题
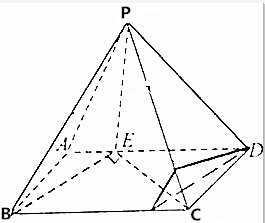 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
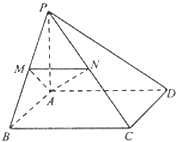 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
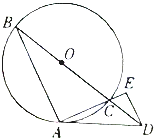 如图,BC为圆O的直径,A为圆O上一点,过点A的直线与圆O相切,且与线段BC的延长线交于点D,E为线段AC延长线上的一点,且ED∥AB.
如图,BC为圆O的直径,A为圆O上一点,过点A的直线与圆O相切,且与线段BC的延长线交于点D,E为线段AC延长线上的一点,且ED∥AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com