
分析 (I)将a=1代入,不等式化为具体的绝对值不等式,然后讨论解之;
(Ⅱ)由题知f(a)=|a|,f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,得证.
解答 解:(Ⅰ)因为a=1,不等式变为|x-2|+|x-1|>3,-----1
当x>2时,有2x-3>3,
∴x>3-----2
当1≤x≤2时,有2-x+x-1>3,
∴x∈φ-------3
当x<1时,有3-2x>3,
∴x<0--------4
所以该不等式的解集为(-∞,0)∪(3,+∞)------5
证明:(Ⅱ)由题知f(a)=|a|,
f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|------7
≥|2a-b+b-a|=|a|-------8
即f(b)≥f(a),
所以等号成立的条件是:当且仅当2a-b与b-a同号或它们至少有一个为零.---10
点评 本题考查了绝对值不等式的解法,考查了讨论的数学思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
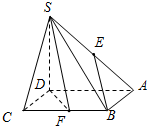 在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,
在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com