
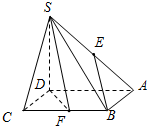
 在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,
在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,分析 (Ⅰ)取SD的中点Q,连接QF、QE,证明BFQE为平行四边形,可得BE∥QF,即可证明:BE∥平面SDF;
(Ⅱ)若AB=5,利用等体积方法求点E到平面SDF的距离.
解答  证明:(Ⅰ)取SD的中点Q,连接QF、QE,
证明:(Ⅰ)取SD的中点Q,连接QF、QE,
由于点E为侧棱AS的中点,Q为SD的中点
故在△DAS中,QE$\underline{\underline{∥}}\frac{1}{2}AD$,
由于F是BC的中点
故BF$\underline{\underline{∥}}\frac{1}{2}AD$,
故QE$\underline{\underline{∥}}BF$
故BFQE为平行四边形
故BE∥QF,又QF?平面EFD1,BE?平面EFD1
故BE∥平面SDF;
解:(Ⅱ)由DS⊥面ABCD,
又AB?面ABCE,故DS⊥AB
又AB⊥AD,故AB⊥面ADS,又BC∥面ADS
故F到面ADS的距离为AB的长,即为5.
设点E到平面SDF的距离为h.
又VF-SED=VE-SDF故$\frac{5}{3}•{\frac{5}{4}^2}=\frac{1}{3}h•{\frac{{\sqrt{5}×5}}{4}^2}$
$h=\sqrt{5}$
点评 本题考查线面平行的判定,考查等体积方法求点到平面的距离,考查学生的计算能力,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
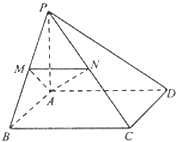 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com