
 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.分析 (1)由正方体的平面展开图及该正方体的直观图的示意图得到正方体为正方体ABCD-EFGH,由AC∥EG,AH∥BG,得到平面BEG∥平面ACH;
(2)由HF∥BD,得∠PDB是正方体中DP与HF所成角(或所成角的补角),由此利用余弦定理能求出正方体中DP与HF所成角的余弦值.
解答 解:(1)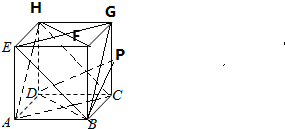 平面BEG∥平面ACH.
平面BEG∥平面ACH.
证明如下:
由正方体的平面展开图及该正方体的直观图的示意图得到正方体为正方体ABCD-EFGH,
∵AC∥EG,AH∥BG,AC∩AH=A,EG∩BG=G,
AC、AH?平面ACH,EG、BG?平面BEG,
∴平面BEG∥平面ACH.
(2)∵HF∥BD,∴∠PDB是正方体中DP与HF所成角(或所成角的补角),
连结PB,设正方形的棱长为2,
则BD=2$\sqrt{2}$,PB=PD=$\sqrt{4+1}$=$\sqrt{5}$,
∴cos∠PDB=$\frac{D{P}^{2}+B{D}^{2}-P{B}^{2}}{2DP•DB}$=$\frac{5+8-5}{2•\sqrt{5}•\sqrt{8}}$=$\frac{\sqrt{10}}{5}$.
∴正方体中DP与HF所成角的余弦值为$\frac{\sqrt{10}}{5}$.
点评 本题考查面面位置关系的判断,考查正方体中异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意余弦定理的合理运用.


科目:高中数学 来源: 题型:解答题
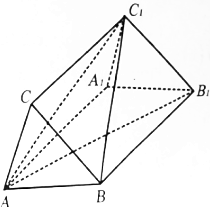 如图,直三棱柱ABC-A1B1C1的底边是边长为2的正三角形.
如图,直三棱柱ABC-A1B1C1的底边是边长为2的正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
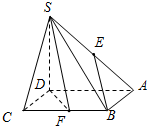 在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,
在底面为正方形的四棱锥S-ABCD中,AD⊥平面ABCD,E、F是AS、BC的中点,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{3}{2}$] | B. | (0,$\frac{9}{4}$] | C. | (0,3] | D. | (0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com