
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 把直线l的参数方程化为普通方程,利用斜率与倾斜角的关系、同角三角函数基本关系式即可得出.
解答 解:由题意得,设直线l倾斜角为θ,直线l的参数方程为$\left\{{\begin{array}{l}{x=1+3t}\\{y=2-4t}\end{array}}\right.$(t为参数),
可化为$y-2=-\frac{4}{3}(x-1)$,则$tanθ=-\frac{4}{3}$,
∵θ∈(0,π),
∴$cosθ=-\frac{3}{{\sqrt{{3^2}+{4^2}}}}=-\frac{3}{5}$,
故选:B.
点评 本题考查了参数方程化为普通方程、斜率与倾斜角的关系、同角三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
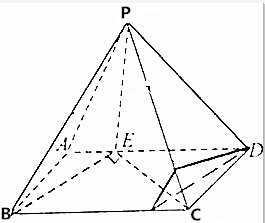 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,正方形ABCD的边长等于2,等腰三角形PAB中PA=PB,且平面PAB⊥平面ABCD,若直线PD与平面ABCD所成的角为$\frac{π}{4}$,则PA的长为( )
如图,正方形ABCD的边长等于2,等腰三角形PAB中PA=PB,且平面PAB⊥平面ABCD,若直线PD与平面ABCD所成的角为$\frac{π}{4}$,则PA的长为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2$\sqrt{6}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sinx | B. | y=9sin4x | C. | y=sin4x | D. | y=9sinx |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{2}}$) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | [$\frac{1}{2}$,1) | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com