
分析 利用配方法求出指数上的二次三项式的范围,结合指数函数的单调性求得值域,再由复合函数的单调性求得原函数的单调增区间.
解答 解:令t=${x}^{2}-2x+\frac{1}{2}$,
则y=0.25${\;}^{{x}^{2}-2x+\frac{1}{2}}$=g(t)=0.25t,
由t=${x}^{2}-2x+\frac{1}{2}$=$(x-1)^{2}-\frac{1}{2}$$≥-\frac{1}{2}$,
∴g(t)=0.25t∈(0,2];
∵t=${x}^{2}-2x+\frac{1}{2}$在(-∞,1]上为减函数,且g(t)=0.25t为减函数,
∴函数y=0.25${\;}^{{x}^{2}-2x+\frac{1}{2}}$的增区间为(-∞,1].
故答案为:(0,2],(-∞,1].
点评 本题考查与指数函数有关的复合函数的单调性和值域的求法,属中档题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
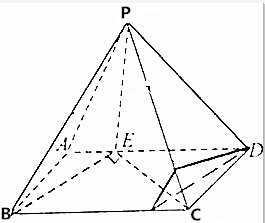 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,PE⊥平面ABCD,垂足E在线段AD上.且AE=$\frac{1}{3}$ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
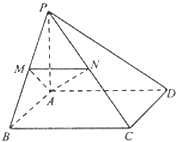 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,点M,N分别为线段PB,PC 上的点,MN⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com