Question

17．已知F是双曲线C：$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，P是y轴正半轴上一点，以OP为直径的圆在第一象限与双曲线的渐近线交于点M，若点P，M，F三点共线，且△MFO的面积是△PMO面积的7倍，则双曲线C的离心率为2$\sqrt{2}$．

Answer 1

分析 由题意可得|MF|=7|MP|，OM⊥PF，设F（c，0），求出|MF|=b，可得|PM|，在直角三角形POF中，运用射影定理，化简可得c，a的关系，再由离心率公式计算即可得到所求值．

解答 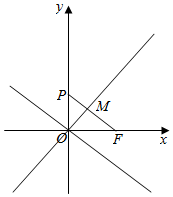解：如图以OP为直径的圆在第一象限与双曲线的渐近线y=$\frac{b}{a}$x交于点M，
由△MFO的面积是△PMO面积的7倍，可得|MF|=7|MP|，
由OM⊥PF，设F（c，0），
可得|MF|=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{bc}{c}$=b，
则|PM|=$\frac{b}{7}$，
在直角三角形POF中，由射影定理可得，
|OF|²=|MF|•|FP|，
即为c²=b•$\frac{8}{7}$b=$\frac{8}{7}$（c²-a²），
则c²=8a²，
即有e=$\frac{c}{a}$=2$\sqrt{2}$．
故答案为：2$\sqrt{2}$．

点评 本题考查双曲线的离心率的求法，注意运用直径所对的圆周角为直角，以及直角三角形的射影定理，考查运算能力，属于中档题．