练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．已知x＞0，y＞0，x+y2=2，则log2x+2log2y的最大值为0．

    分析 由xy2≤（$\frac{x+{y}^{2}}{2}$）2=1，利用log2x+2log2y=$lo{g}_{2}x+lo{g}_{2}{y}^{2}$=$lo{g}_{2}（x{y}^{2}）$，能求出结果．

    解答 解：∵x＞0，y＞0，x+y2=2，
    ∴xy2≤（$\frac{x+{y}^{2}}{2}$）2=1，
    ∴log2x+2log2y=$lo{g}_{2}x+lo{g}_{2}{y}^{2}$=$lo{g}_{2}（x{y}^{2}）$≤log21=0．
    故答案为：0．

    点评 本题考查代数式的最大值的求法，是基础题，解题时要认真审题，注意基本不等式、对数性质及运算法则的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．已知数列{an}的前n项和为Sn，且满足a1=1，an•an+1=2Sn，设bn=$\frac{{a}_{n}}{{3}^{{a}_{n}}}$，若存在正整数p，q（p＜q），使得b1，bp，bq成等差数列，则p+q=5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知实数x、y满足$\left\{\begin{array}{l}{2x-y+1≥0}\\{x≥1}\\{x-2y+3≤0}\end{array}\right.$，则$\frac{y}{x}$的取值范围为（$\frac{1}{2}$，3]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

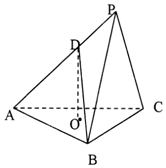    1．三棱锥P-ABC中，底面ABC为等边三角形，O为△ABC的中心，平面PBC⊥平面ABC，PB=PC=BC=$\sqrt{3}$，D为AP上一点，且AD=2DP．
    （I）求证：DO∥平面PBC；
    （II）求证：AC⊥平面OBD；
    （III）求三棱锥B-PDC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．已知直线ax-y=0（a∈R）与圆C：x2+y2-2ax-2y+2=0交于A，B两点，C为圆心，若∠ACB=$\frac{π}{3}$，则圆C的面积为（　　）
    A．8πB．6πC．4πD．2π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知等比数列{an}满足a1+a3=10，a2+a4=5，则a5=（　　）
    A．1B．$\frac{1}{2}$C．$\frac{1}{4}$D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．数列{an}的前n项和为Sn，若Sn+an=4-$\frac{1}{{{2^{n-2}}}}（{n∈{N^*}}）$，则an=$\frac{n}{{2}^{n-1}}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．下面四个条件中，使a＞b成立的必要而不充分条件是（　　）
    A．a-1＞bB．a+1＞bC．|a|＞|b|D．a3＞b3

    查看答案和解析>>

    科目：高中数学 来源：2016-2017学年江西省高一上学期第一次月考数学试卷（解析版） 题型：解答题

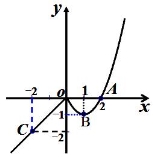
    如图是函数f（x）的图象,OC段是射线,而OBA是抛物线的一部分，试写出f（x）的函数表达式．

    查看答案和解析>>

    同步练习册答案