
分析 Sn+an=4-$\frac{1}{{{2^{n-2}}}}({n∈{N^*}})$,n≥2时,Sn-1+an-1=4-$\frac{1}{{2}^{n-3}}$,可得:2an-an-1=$\frac{1}{{2}^{n-2}}$.变形为2n-1an-2n-2an-1=1.利用等差数列的通项公式即可得出.
解答 解:∵Sn+an=4-$\frac{1}{{{2^{n-2}}}}({n∈{N^*}})$,
∴n≥2时,Sn-1+an-1=4-$\frac{1}{{2}^{n-3}}$,
可得:2an-an-1=$\frac{1}{{2}^{n-2}}$.
∴2n-1an-2n-2an-1=1.
n=1时,2a1=4-2,解得a1=1.
∴数列{2n-1an}是等差数列,首项为1,公差为1.
则2n-1an=1+(n-1)=n.
∴an=$\frac{n}{{2}^{n-1}}$.
故答案为:$\frac{n}{{{2^{n-1}}}}$.
点评 本题考查了数列递推公式、等差数列的通项公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{3}{7}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
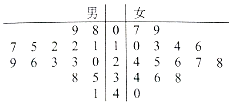 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ②③ | C. | ①③ | D. | ③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com