
 ijѧУ�ü��������������ȡ��30��ͬѧ������ÿ��ƽ�������Ķ�ʱ�䣨��λ��Сʱ�����е��飬��Ҷͼ��ͼ�������¾������Ķ�ʱ�䲻����30Сʱ��ѧ����Ϊ�������ԡ���
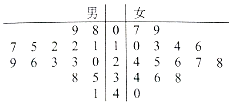
ijѧУ�ü��������������ȡ��30��ͬѧ������ÿ��ƽ�������Ķ�ʱ�䣨��λ��Сʱ�����е��飬��Ҷͼ��ͼ�������¾������Ķ�ʱ�䲻����30Сʱ��ѧ����Ϊ�������ԡ������� ��1�����У900��ѧ���С������ԡ���x�ˣ����õȿ����¼����ʼ��㹫ʽ�г����̣��������У900��ѧ���С������ԡ�Լ�ж����ˣ�
��2�����������ȡ���С������ԡ�Ϊa35��a38��a41����ȡ��Ů�������ԡ�Ϊb34��b36��b38��b40�������½DZ��ʾ������ƽ�������Ķ�ʱ�䣩���ɴ������оٷ���ͬ��7���������ԡ��������ȡ�С�Ů�����Ը�1�˵IJ�ͬ�ij�ȡ������������
��������A��ʾ�¼�����ȡ���С�Ů��λ�������¾�����ʱ��������2Сʱ���������оٷ�����¼�A�����Ļ����¼��������ɴ��������ȡ���С�Ů��λ�������ԡ��¾�����ʱ��������2Сʱ�ĸ��ʣ�
��� �⣺��1�����У900��ѧ���С������ԡ���x�ˣ�
��$\frac{7}{30}=\frac{x}{900}$�����x=210��
���Ը�У900��ѧ���С������ԡ�Լ��210�ˣ�
��2�����������ȡ���С������ԡ�Ϊa35��a38��a41��
��ȡ��Ů�������ԡ�Ϊb34��b36��b38��b40�������½DZ��ʾ������ƽ�������Ķ�ʱ�䣩��
���7���������ԡ��������ȡ�С�Ů�����Ը�1�˵����л����¼�Ϊ��
��a35��b34������a35��b36������a35��b38������a35��b40������a38��b34������a38��b36����
��a38��b38������a38��b40������a41��b34������a41��b36������a41��b38������a41��b40����
���Թ���12�ֲ�ͬ�ij�ȡ������
��������A��ʾ�¼�����ȡ���С�Ů��λ�������¾�����ʱ��������2Сʱ����
���¼�A��������a35��b34������a35��b36������a38��b36������a38��b38����
��a38��b40������a41��b40����6�������¼���
���Գ�ȡ���С�Ů��λ�������ԡ��¾�����ʱ��������2Сʱ�ĸ���$P��A��=\frac{6}{12}=\frac{1}{2}$��
���� ���⿼�龥Ҷͼ�����ʡ��оٷ��Ȼ���֪ʶ������������֤����������������������鼯��˼�롢������ת��˼�룬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{{a}^{2}}{2}$ | B�� | $\frac{{a}^{2}}{2}$ | C�� | -2a2 | D�� | a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
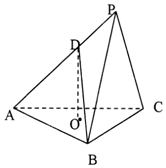 ����P-ABC�У�����ABCΪ�ȱ������Σ�OΪ��ABC�����ģ�ƽ��PBC��ƽ��ABC��PB=PC=BC=$\sqrt{3}$��DΪAP��һ�㣬��AD=2DP��
����P-ABC�У�����ABCΪ�ȱ������Σ�OΪ��ABC�����ģ�ƽ��PBC��ƽ��ABC��PB=PC=BC=$\sqrt{3}$��DΪAP��һ�㣬��AD=2DP���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\frac{1}{2}$ | C�� | $\frac{1}{4}$ | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 1 | C�� | 0 | D�� | -4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-1��b | B�� | a+1��b | C�� | |a|��|b| | D�� | a3��b3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2+i | B�� | 2-i | C�� | 5-i | D�� | 5+i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�����ʡ�����и߶���ѧ����ѧ����ѧ���������棩 ���ͣ������
�躯��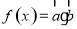 ����������
���������� ��
��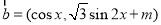 ��
��
��1������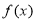 ����С�����ں�
����С�����ں�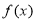 ��
��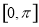 �ϵĵ����������䣻
�ϵĵ����������䣻
��2���� ʱ��
ʱ��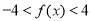 ���������ʵ��
���������ʵ��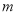 ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com