
| A. | -$\frac{{a}^{2}}{2}$ | B. | $\frac{{a}^{2}}{2}$ | C. | -2a2 | D. | a2 |
分析 作出图形,依题意可得$\overrightarrow{EB}$+$\overrightarrow{EC}$=2$\overrightarrow{ED}$=$\overrightarrow{AD}$,$\overrightarrow{EA}$=(-$\frac{1}{2}$)$\overrightarrow{AD}$,再利用平面向量的数量积即可得答案.
解答 解:∵E为AD中点,AD=a,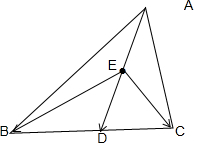
∴$\overrightarrow{EB}$+$\overrightarrow{EC}$=2$\overrightarrow{ED}$=$\overrightarrow{AD}$,
∴($\overrightarrow{EB}$+$\overrightarrow{EC}$)•$\overrightarrow{EA}$=$\overrightarrow{AD}$•$\overrightarrow{EA}$=$\overrightarrow{AD}$•(-$\frac{1}{2}$)$\overrightarrow{AD}$=-$\frac{1}{2}$${\overrightarrow{AD}}^{2}$=-$\frac{1}{2}$a2,
故选:A.
点评 本题考查平面向量的数量积的运算,求得$\overrightarrow{EB}$+$\overrightarrow{EC}$=2$\overrightarrow{ED}$=$\overrightarrow{AD}$是关键,考查作图与运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -$\frac{3}{4}$ | D. | -$\frac{11}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
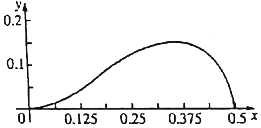 函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )
函数f(x)=axm(1-2x)n(a>0)在区间[0,$\frac{1}{2}$]上的图象如图所示,则m、n的值可能是( )| A. | m=1,n=1 | B. | m=1,n=2 | C. | m=2,n=3 | D. | m=3,n=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
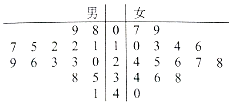 某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.
某学校用简单随机抽样方法抽取了30名同学,对其每月平均课外阅读时间(单位:小时)进行调查,茎叶图如图:若将月均课外阅读时间不低于30小时的学生称为“读书迷”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com