
| A. | (-2,0)∪(2,+∞) | B. | (-2,0)∪(0,2) | C. | (-∞,-2)∪(2,+∞) | D. | (-∞,-2)∪(0,2) |
分析 当x<0时,F′(x)=[$\frac{f(x)}{g(x)}$]′=$\frac{{f}^{'}(x)g(x)-f(x){g}^{'}(x)}{[g(x)]^{2}}$<0,从而F(x)在(-∞,0)上单调递减,在(0,+∞)单调递增,利用f(2)=0,得到F(-2)=F(2)=0,由此能求出F(x)<0的解集.
解答 解:∵F(x)=$\frac{f(x)}{g(x)}$是(-∞,0)∪(0,+∞)上的偶函数,
∴f(x)和g(x)同为偶函数或同为奇函数,
当f(x)和g(x)同为偶函数时,f(-x)=f(x),g(-x)=g(x),
当f(x)和g(x)同为奇函数时,f(-x)=-f(x),g(-x)=-g(x),
∵当x<0时,f′(x)g(x)-f(x)g′(x)<0
∴当x<0时,F′(x)=[$\frac{f(x)}{g(x)}$]′=$\frac{{f}^{'}(x)g(x)-f(x){g}^{'}(x)}{[g(x)]^{2}}$<0,
∴F(x)在(-∞,0)上单调递减
∵F(x)为偶函数,
根据偶函数的性质可得函数F(x)在(0,+∞)单调递增,
又f(2)=0,∴f(-2)=0,∴F(-2)=F(2)=0
F(x)<0的解集为(-2,0)∪(0,2).
故选:B.
点评 本题考查导数的性质及应用、函数的奇偶性、单调性等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{6}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{{a}^{2}}{2}$ | B. | $\frac{{a}^{2}}{2}$ | C. | -2a2 | D. | a2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
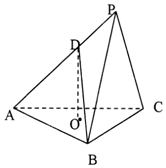 三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.
三棱锥P-ABC中,底面ABC为等边三角形,O为△ABC的中心,平面PBC⊥平面ABC,PB=PC=BC=$\sqrt{3}$,D为AP上一点,且AD=2DP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com