
(本题满分14分)已知圆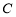 :
: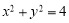 .
.
(Ⅰ)直线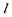 过点
过点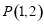 ,且与圆
,且与圆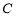 交于
交于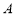 、
、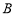 两点,若
两点,若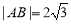 ,求直线
,求直线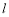 的方程;
的方程;
(Ⅱ)过圆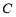 上一动点
上一动点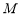 作平行于
作平行于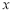 轴的直线
轴的直线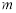 ,设
,设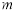 与
与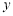 轴的交点为
轴的交点为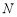 ,若向量
,若向量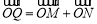 ,求动点
,求动点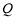 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
(Ⅰ)x=1,3x-4y+5=0,;
(Ⅱ)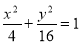 (y≠0)轨迹为长轴长为8,短轴长为4,焦距为4
(y≠0)轨迹为长轴长为8,短轴长为4,焦距为4 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
【解析】
试题分析:(Ⅰ)由直线与圆位置关系得:半径,半弦长,圆心到直线距离构成勾股,即 ,因此d=1,又直线
,因此d=1,又直线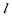 过点
过点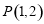 ,故利用直线方程点斜式求解,注意先讨论斜率不存在情况:若
,故利用直线方程点斜式求解,注意先讨论斜率不存在情况:若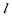 ⊥x轴,直线方程为x=1,A(1,-
⊥x轴,直线方程为x=1,A(1,-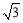 ),B(1,
),B(1,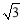 ),
),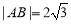 ,适合;若
,适合;若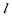 的斜率存在,设
的斜率存在,设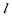 的方程为y=k(x-1)+2,圆心到直线的距离为d=1=
的方程为y=k(x-1)+2,圆心到直线的距离为d=1= 解得k=
解得k=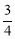 ,直线方程为3x-4y+5=0,(Ⅱ)相关点法求轨迹方程:先找出所求的与已知动点之间关系,代入已知动点轨迹,化简即得所求动点轨迹方程:设M(
,直线方程为3x-4y+5=0,(Ⅱ)相关点法求轨迹方程:先找出所求的与已知动点之间关系,代入已知动点轨迹,化简即得所求动点轨迹方程:设M(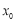 ,
,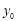 )(
)(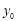 ≠0).则N(0,
≠0).则N(0,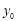 ),Q(x,y),则
),Q(x,y),则  ,又
,又 ,动点Q的轨迹方程为
,动点Q的轨迹方程为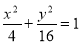 (y≠0)轨迹为长轴长为8,短轴长为4,焦距为4
(y≠0)轨迹为长轴长为8,短轴长为4,焦距为4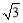 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点
试题解析:【解析】
(Ⅰ)若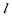 ⊥x轴,直线方程为x=1,A(1,-
⊥x轴,直线方程为x=1,A(1,-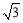 ),B(1,
),B(1,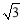 ),
),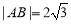 ,适合---3分
,适合---3分
若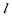 的斜率存在,设
的斜率存在,设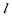 的方程为y=k(x-1)+2,圆心到直线的距离为d=
的方程为y=k(x-1)+2,圆心到直线的距离为d= ,圆半径为2,故
,圆半径为2,故 ,k=
,k=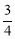 ,直线方程为3x-4y+5=0, ------7分
,直线方程为3x-4y+5=0, ------7分
综上所求直线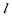 的方程为x=1,3x-4y+5=0,; -----8分
的方程为x=1,3x-4y+5=0,; -----8分
(Ⅱ)设M(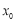 ,
,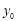 )(
)(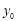 ≠0).则N(0,
≠0).则N(0,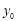 ),Q(x,y),则
),Q(x,y),则  ----2分
----2分
又 ,动点Q的轨迹方程为
,动点Q的轨迹方程为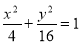 (y≠0) -----5分
(y≠0) -----5分
轨迹为长轴长为8,短轴长为4,焦距为4 且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点.----6分
且焦点在y轴上的椭圆且去掉椭圆短轴的两个端点.----6分
考点:直线与圆位置关系,轨迹方程


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源:2014-2015学年江苏省等五校高三12月第一次联考文科数学试卷(解析版) 题型:解答题
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈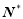 )名员工从事第三产业,调整后他们平均每人每年创造利润为
)名员工从事第三产业,调整后他们平均每人每年创造利润为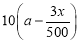 万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
万元(a>0),剩下的员工平均每人每年创造的利润可以提高0.2x%.
(1)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(2)在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:解答题
选修4-4:坐标系与参数方程
已知曲线 的参数方程为
的参数方程为 ,曲线
,曲线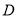 的极坐标方程为
的极坐标方程为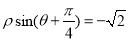 .
.
(1)将曲线 的参数方程化为普通方程;
的参数方程化为普通方程;
(2)曲线 与曲线
与曲线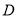 有无公共点?试说明理由.
有无公共点?试说明理由.
查看答案和解析>>
科目:高中数学 来源:2015届江苏教育学院附属高中高三上学期期中理科数学试卷(解析版) 题型:填空题
给出以下四个命题:
①已知命题 ;命题
;命题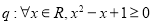 .则命题
.则命题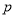 和
和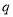 都是真命题;
都是真命题;
②过点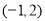 且在
且在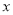 轴和
轴和 轴上的截距相等的直线方程是
轴上的截距相等的直线方程是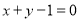 ;
;
③函数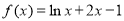 在定义域内有且只有一个零点;
在定义域内有且只有一个零点;
④先将函数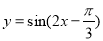 的图像向右平移
的图像向右平移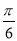 个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为
个单位,再将新函数的周期扩大为原来的两倍,则所得图像的函数解析式为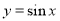 .
.
其中正确命题的序号为 .(把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年浙江省嘉兴市高三新高考单科综合调研三文科数学试卷(解析版) 题型:选择题
函数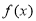 的定义域为
的定义域为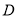 ,若满足:
,若满足:
① 在
在 内是单调函数;
内是单调函数;
②存在 ,使
,使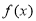 在
在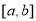 上的值域为
上的值域为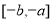 ,那么
,那么 叫做对称函数.
叫做对称函数.
现有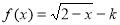 是对称函数,那么
是对称函数,那么 的取值范围是( )
的取值范围是( )
A.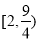 B.
B.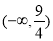 C.
C.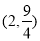 D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com