
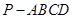 中,
中,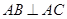 ,
,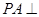 平面
平面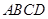 ,且
,且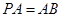 ,点
,点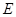 是
是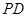 的中点.
的中点.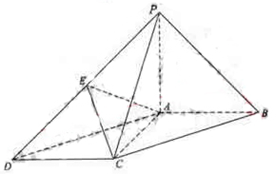
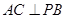 ;
;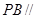 平面
平面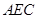 ;
;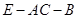 的大小.
的大小.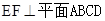 ,进而找出二面角的平面角
,进而找出二面角的平面角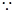
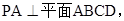
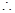 AB是PB在平面ABCD上的射影,
AB是PB在平面ABCD上的射影,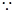 AB
AB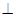 AC,AC
AC,AC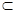 平面ABCD,
平面ABCD,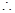 AC
AC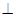 PB.
PB.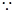 ABCD是平行四边形
ABCD是平行四边形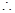 O是BD的中点又E是PD的中点,
O是BD的中点又E是PD的中点,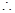 EO
EO PB.又PB
PB.又PB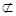 平面AEC,EO
平面AEC,EO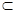 平面AEC,
平面AEC,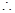 PB
PB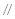 平面AEC,
平面AEC,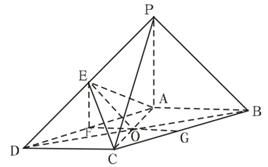
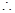 EF
EF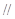 PA又
PA又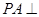 平面
平面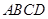 ,
,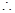
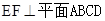
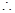 FO
FO AB
AB FO^AC,由三垂线定理可知
FO^AC,由三垂线定理可知 ÐEOF是二面角E-AC-D的平面角.又FO=
ÐEOF是二面角E-AC-D的平面角.又FO=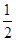 AB=
AB=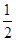 PA=EF。
PA=EF。 ÐEOF=45°而二面角
ÐEOF=45°而二面角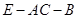 与二面角E-AC-D互补,
与二面角E-AC-D互补,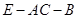 的大小为135°.
的大小为135°.

科目:高中数学 来源:不详 题型:解答题
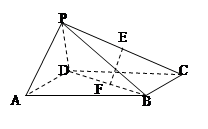
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.存在一条直线a,a∥α,a∥β |
| B.存在一条直线a,a?α,a∥β |
| C.存在两条平行直线a,b,a?α,b?β,a∥β,b∥α |
| D.存在两条异面直线a,b,a?α,b?β,a∥β,b∥α |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若l//α,l//β,则α//β |
| B.若l//α,l⊥β,则α⊥β |
| C.若α⊥β,l⊥α,则l⊥β |
| D.若α⊥β,l//α,则l⊥β |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
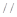 平面
平面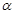 ,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面
,E,F分别是线段AD和BC的中点,当正四面体绕以AB为轴旋转时,线段EF在平面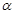 上的射影
上的射影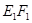 长的范围是( )
长的范围是( )A.[0, ] ] | B.[ , , ] ] |
C.[ , , ] ] | D.[ , , ] ] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
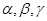 为两两不重合的平面,
为两两不重合的平面,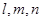 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: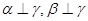 ,则
,则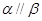 ;
;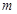
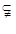
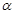 ,
,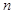
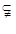
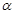 ,
,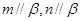 ,则
,则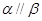 ;
;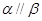 ,
,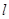
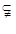
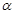 ,则
,则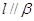 ;
;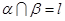 ,
,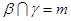 ,
,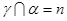 ,
,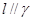 ,则
,则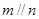 .
.| A.(1)(3) | B.(2)(3) |
| C.(2)(4) | D.(3)(4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com