
分析 分别求出p,q为真时的a的范围,根据若“p∨q”为真命题,“p∧q”为假命题,得到p,q一真一假,从而求出a的范围即可.
解答 解:若命题p为真,即对于任意实数x,都有ax2+2ax+4>0恒成立,
a=0时,4>0成立,
a≠0,只需$\left\{\begin{array}{l}{a>0}\\{△={4a}^{2}-16a<0}\end{array}\right.$,解得:0<a<4,
综上,若p真:a∈[0,4);
若命题q:方程x2+y2-2x+a=0表示一个圆,
只需4-4a>0,解得:a<1,
故,q为真时,a∈(-∞,1);
若“p∨q”为真命题,“p∧q”为假命题,
则p,q一真一假,
故a∈(-∞,0)∪[1,4).
点评 本题考察了函数恒成立问题,考察圆的方程,考察复合命题的判断,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | {α|α=2kπ,k∈Z} | B. | {α|α=kπ,k∈Z} | C. | {α|α=kπ+$\frac{π}{2}$,K∈Z} | D. | {α|α=$\frac{1}{2}kπ$,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{5}{6}$π | D. | $\frac{11}{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
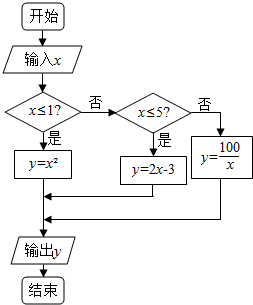 如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.
如图,给出了一个程序框图,其作用是输入x的值,输出相应y的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com