
| A. | $-\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | $-\frac{5}{3}$ |
分析 由条件利用同角三角函数的基本关系,诱导公式、二倍角公式,求得要求式子的值.
解答 解:∵cos(x-$\frac{π}{3}$)=cos($\frac{π}{3}$-x)=$\frac{1}{3}$,
∴cos(2x-$\frac{2π}{3}$)+sin2($\frac{π}{3}$-x)=2${cos}^{2}(x-\frac{π}{3})$-1+[1-${cos}^{2}(\frac{π}{3}-x)$]=2•$\frac{1}{9}$-1+1-$\frac{1}{9}$=$\frac{1}{9}$,
故选:B.
点评 本题主要考查同角三角函数的基本关系,诱导公式、二倍角公式的应用,属于基础题.


 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:选择题
| A. | 0.3 | B. | 0.35 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
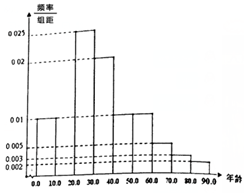 鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.
鹰潭市龙虎山花语世界位于中国第八处世界自然遗产,世界地质公元、国家自然文化双遗产地、国家AAAAA级旅游景区--龙虎山主景区排衙峰下,是一座独具现代园艺风格的花卉公园,园内汇集了3000余种花卉苗木,一年四季姹紫嫣红花香四溢.花园景观融合法、英、意、美、日、中六大经典园林风格,景观设计唯美新颖.玫瑰花园、香草花溪、台地花海、植物迷宫、儿童乐园等景点错落有致,交相呼应又自成一体,是世界园艺景观的大展示.该景区自2015年春建成试运行以来,每天游人如织,郁金香、向日葵、虞美人等赏花旺季日入园人数最高达万人.| 年龄 | 频数 | 频率 | 男 | 女 |
| [0,10) | 10 | 0.1 | 5 | 5 |
| [10,20) | ① | ② | ③ | ④ |
| [20,30) | 25 | 0.25 | 12 | 13 |
| [30,40) | 20 | 0.2 | 10 | 10 |
| [40,50) | 10 | 0.1 | 6 | 4 |
| [50,60) | 10 | 0.1 | 3 | 7 |
| [60,70) | 5 | 0.05 | 1 | 4 |
| [70,80) | 3 | 0.03 | 1 | 2 |
| [80,90) | 2 | 0.02 | 0 | 2 |
| 合计 | 100 | 1.00 | 45 | 55 |
| 50岁以上 | 50岁以下 | 合计 | |
| 男生 | 5 | 40 | 45 |
| 女生 | 15 | 40 | 55 |
| 合计 | 20 | 80 | 100 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤4} | B. | {0,1,2,3} | C. | {0,1,2,3,4} | D. | {1,2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e-1 | B. | 1-e | C. | $1-\frac{1}{e}$ | D. | $\frac{1}{e}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x∈R|0<x<1} | B. | {x∈R|0<x<2} | C. | {x∈R|-1<x<0} | D. | {x∈R|-1<x<2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com