
分析 (Ⅰ)先求导,再分类讨论,根据导数和函数的单调性的关系即可解决,
(Ⅱ)根据题意可得f(x2)-x22)<f(x1)-x12,构造函数,再求导,再分离参数,利用导数求出函数的最值即可.
解答 解:(Ⅰ)f(x)=$\frac{1}{2}{x^2}$+mx+mlnx的定义域为(0,+∞),
∴f′(x)=x+m+$\frac{m}{x}$=$\frac{{x}^{2}+mx+m}{x}$,
当m≥0时,f′(x)>0,函数f(x)在(0,+∞)上单调递增,
当m<0时,方程x2+mx+m=0的判别式为△=m2-4m>0,
令f′(x)>0,解得x>$\frac{-m+\sqrt{{m}^{2}-4m}}{2}$,令f′(x)<0,解得0<x<$\frac{-m+\sqrt{{m}^{2}-4m}}{2}$,
∴当m<0时,f(x)在($\frac{-m+\sqrt{{m}^{2}-4m}}{2}$,+∞)单调递增,在(0,$\frac{-m+\sqrt{{m}^{2}-4m}}{2}$)上单调递减,
(Ⅱ)当m>0,函数f(x)在(0,+∞)上单调递增,
∵[1,2]?(0,+∞),
∴函数f(x)在[1,2]上单调递增,
∵x1<x2,
∴f(x2)-f(x1)>0,
由题意可得f(x2)-f(x1)<x22-x12,
整理可得f(x2)-x22)<f(x1)-x12,
令g(x)=f(x)-x2=-$\frac{1}{2}{x^2}$+mx+mlnx,
则g(x)在[1,2]上单调递减,
∴g′(x)=-x+m+$\frac{m}{x}$=$\frac{-{x}^{2}+mx+m}{x}$≤0恒成立,
∴m≤$\frac{{x}^{2}}{1+x}$,
令h(x)=$\frac{{x}^{2}}{1+x}$,
则h′(x)=$\frac{2x(1+x)-{x}^{2}}{(1+x)^{2}}$=$\frac{{x}^{2}+2x}{(1+x)^{2}}$>0,
∴h(x)在[1,2]上单调递增,
∴h(x)min=h(1)=$\frac{1}{2}$,
∴m≤$\frac{1}{2}$
点评 本题考查了导数和函数的单调性和和最值的关系,考查了的学生的运算能力和转化能力和分类讨论的能力,属于中档题


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 2n+n | B. | 2n+1-1 | C. | $\frac{{{3^{n+1}}-3n}}{2}$ | D. | $\frac{{{3^{n+1}}-3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
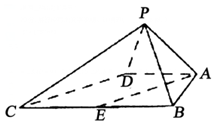 如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | $-\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 34种 | B. | 48种 | C. | 96种 | D. | 144种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com