练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知随机变量ξ服从正态分布N（μ，σ2），若P（ξ＜2）=P（ξ＞6）=0.15，则P（2≤ξ＜4）等于（　　）
    A．0.3B．0.35C．0.5D．0.7

    分析 随机变量ξ服从正态分布N（μ，σ2），若P（ξ＜2）=P（ξ＞6）=0.15，得到曲线关于x=4对称，根据曲线的对称性从而得到所求．

    解答 解：由题意可得$P（2≤ξ＜4）=\frac{1-0.15×2}{2}=0.35$，
    故选：B．

    点评 本题考查正态分布曲线的特点及曲线所表示的意义，考查概率的性质，是一个基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    12．已知数列{an}的前n项和为Sn，且an=4n，若不等式Sn+8≥λn对任意的n∈N*都成立，则实数λ的取值范围为（-∞，10]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

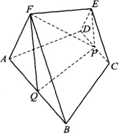    13．如图，在五面体ABCDEF中，面CDE和面ABF都为等边三角形，面ABCD是等腰梯形，点P、Q分别是CD、AB的中点，FQ∥EP，PF=PQ，AB=2CD=2．
    （1）求证：平面ABF⊥平面PQFE；
    （2）若PQ与平面ABF所成的角为$\frac{π}{3}$，求三棱锥P-QDE的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．下列结论正确的是④．
    ①（x2-4x）（x+$\frac{1}{x}$）9的展开式中x2的系数为-210；
    ②在吸烟与患肺病这两个分类变量的计算中，从独立性检验知，有99%的把握认为吸烟与患病有关系时，我们说某人吸烟，那么他有99%的可能患肺病；
    ③已知命题“若函数f（x）=ex-mx在（0，+∞）上是增函数，则m≤1”的逆否命题是“若m＞1，则函数f（x）=ex-mx在（0，+∞）上是减函数”，是真命题；
    ④不等式ax2-（2a-3）x-1＞0对?x＞1恒成立的充要条件是0≤a≤2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

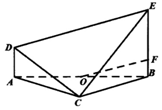    17．如图，在以A、B、C、D、E为顶点的五面体中，AD⊥平面ABC，AD∥BE，AC⊥CB，AB=2BE=4AD=4．
    （1）O为AB的中点，F是线段BE上的一点，BE=4BF，证明：OF∥平面CDE；
    （2）当直线DE与平面CBE所成角的正切值为$\frac{2\sqrt{2}}{3}$时，求平面CDE与平面ABC所成锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知递增数列{an}对任意n∈N*均满足an∈N*，aan=3n，记${b_n}={a_{2•{3^{n-1}}}}$（n∈N*），则数列{bn}的前n项和等于（　　）
    A．2n+nB．2n+1-1C．$\frac{{{3^{n+1}}-3n}}{2}$D．$\frac{{{3^{n+1}}-3}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．社区服务是综合实践活动课程的重要内容．上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据，按时间段[65，70），[70，75），[75，80），[80，85），[85，90）（单位：小时）进行统计，其频率分布直方图如图所示．
    （Ⅰ）求抽取的200位学生中，参加社区服务时间不少于80小时的学生人数，并估计从全市高中学生中任意选取一人，其参加社区服务时间不少于80小时的概率；
    （Ⅱ）从全市高中学生中任意选取3位学生，记ξ为3名学生中参加社区服务时间不少于80小时的人数，试求随机变量ξ的分布列和数学期望Eξ和方差Dξ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知直线m，n与平面α，β，γ满足α⊥β，α∩β=m，n⊥α，n?γ，则下列判断一定正确的是（　　）
    A．m∥γ，α⊥γB．n∥β，α⊥γC．β∥γ，α⊥γD．m⊥n，α⊥γ

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．已知cos（x-$\frac{π}{3}$）=$\frac{1}{3}$，则cos（2x-$\frac{2π}{3}$）+sin2（$\frac{π}{3}$-x）的值为（　　）
    A．$-\frac{1}{9}$B．$\frac{1}{9}$C．$\frac{5}{3}$D．$-\frac{5}{3}$

    查看答案和解析>>

    同步练习册答案