
分析 ①,(x2-4x)(x+$\frac{1}{x}$)9的展开式中x2项是(x+$\frac{1}{x}$)9的中的一次项与-4x积,即可求出系数加以判断;
②,有99%的把握认为吸烟与患肺病有关系,表示有1%的可能性使推断出现错误,不表示有99%的可能患有肺病,也不表示在100个吸烟的人中必有99人患有肺病,故可得结论.
③,“增函数”的否定不是“减函数”;
④、当a=0时,满足条件;当a≠0时,必须满足 f(1)=-a-2≥0,a>0,$\frac{2a-3}{a}≤1$⇒0<a≤2
解答 解:对于①,(x2-4x)(x+$\frac{1}{x}$)9的展开式中x2项是(x+$\frac{1}{x}$)9的中的一次项与-4x积,即-4x•${C}_{9}^{5}{x}^{5}(\frac{1}{x})^{9-5}=-4{×C}_{9}^{4}{x}^{2}=-504{x}^{2}$,系数为-504,故错;
对于②,有99%的把握认为吸烟与患肺病有关系,即有1%的可能性使推断出现错误,不表示有99%的可能患有肺病,也不表示在100个吸烟的人中必有99人患肺病,故不正确;
对于③,已知命题“若函数f(x)=ex-mx在(0,+∞)上是增函数,则m≤1”的逆否命题是“若m>1,则函数f(x)=ex-mx在(0,+∞)上不是增函数”,故错;
对于④,不等式ax2-(2a-3)x-1>0对?x>1恒成立的充要条件是:
当a=0时,满足条件;当a≠0时,必须满足 f(1)=-a-2≥0,a>0,$\frac{2a-3}{a}≤1$⇒0<a≤2
不等式ax2-(2a-3)x-1>0对?x>1恒成立的充要条件是0≤a≤2成立,故正确.
故答案为:④.
点评 本题考查了命题真假的判定,需要掌握大量的基础知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.3 | B. | 0.35 | C. | 0.5 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
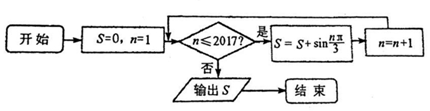
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤4} | B. | {0,1,2,3} | C. | {0,1,2,3,4} | D. | {1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com