
分析 根据题意,分2种情况讨论:①、取出的3个数字中不含0,先在1,2,3,4,5,6,7中任取3个数,再分析每种取法的“伞数”数目,由分步计数原理可得此时的“伞数”数目,②、取出的3个数字中含有0,同①可得其“伞数”数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、取出的3个数字中不含0,
先在1,2,3,4,5,6,7中任取3个数,有C73=35种取法,
把最大的数放在十位,剩下的2个数全排列,放在百位、个位,有A22=2种情况,
则此时一共有35×2=70个“伞数”,
②、取出的3个数字中含有0,
需要在1,2,3,4,5,6,7中任取2个数,有C72=21种取法,
把最大的数放在十位,0放在个位,剩下的数放在百位,有1种情况,
则此时一共有21×1=21个“伞数”,
则一共有70+21=91个“伞数”,
故答案为:91.
点评 本题考查排列、组合的应用,注意0不能在百位,需要对0进行分类讨论.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
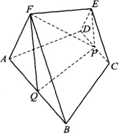 如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.
如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n+n | B. | 2n+1-1 | C. | $\frac{{{3^{n+1}}-3n}}{2}$ | D. | $\frac{{{3^{n+1}}-3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
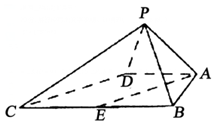 如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.
如图,四棱锥P-ABCD中,∠ABC=BAD=90°,BC=2AD,△PAB与△PAD都是边长为2的等边三角形,E是BC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com