
分析 欲求满足x+y≤4的点的个数,先在直角坐标系中画出满足x+y≤4的平面区域,后在区域中一一找出整数点即可.再根据归纳推理即可求出答案
解答 解:如图所示,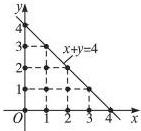 用数形结合法知共有15个满足x+y≤4的点P.
用数形结合法知共有15个满足x+y≤4的点P.
分别为 (0,0),
(1,0),(0,1),
(2,0),(1,1),(0,2),
(3,0),(2,1),(1,2),(0,3),
(4,0),(3,1),(2,2),(1,3),(0,4),
共有1+2+3+4+5=15个
当n=1时,1+2=3个,
当n=2时,1+2+3=6个,
当n=3时,1+2+3+4=10个,
…
一般地,满足x+y≤n(n∈N)的点P的个数应为1+2+3+…+(n+1)=$\frac{(n+1)(n+2)}{2}$
故答案为:15,$\frac{(n+1)(n+2)}{2}$
点评 借助于平面区域特性,用几何方法处理代数问题,以及归纳推理的问题,体现了数形结合思想、化归思想.属于中档题.


 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
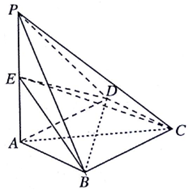 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com