
分析 由直线x+ay-1=0与2x+4y-3=0平行,求出a=2,由此利用分类讨论思想能求出${({x+\frac{1}{x}-a})^5}$=(x+$\frac{1}{x}$-2)5的展开式中x的系数.
解答 解:∵直线x+ay-1=0与2x+4y-3=0平行,
∴$\frac{1}{2}=\frac{a}{4}≠\frac{-1}{-3}$,解得a=2,
∴${({x+\frac{1}{x}-a})^5}$=(x+$\frac{1}{x}$-2)5,
∴展开式中x的系数为:${C}_{5}^{1}{C}_{4}^{4}(-2)^{4}$+${C}_{5}^{2}{C}_{3}^{1}{C}_{2}^{2}(-2)^{2}$+${C}_{5}^{3}{C}_{2}^{2}$=80+120+10=210.
故答案为:210.
点评 本题考查直线与直线平行、二项式定理等基础知识,考查推理论证能力、运算求解能力,考查分类与整合思想、函数与方程思想,是基础题.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:解答题
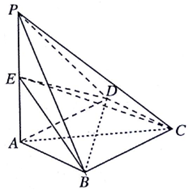 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
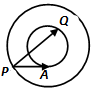 如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1] | B. | (-∞,1) | C. | [1,3) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\sqrt{3}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | 0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com