
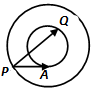
 如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$]. 分析 建立适当的平面直角坐标系,设Q(cosα,sinα),A(0,-1),取P(-$\sqrt{3}$,-1),
利用平面向量的坐标表示求数量积,根据三角函数的有界性求出它的取值范围.
解答 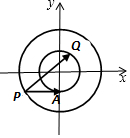 解:建立平面直角坐标系,如图所示,
解:建立平面直角坐标系,如图所示,
设Q(cosα,sinα),A(0,-1),
则P(±$\sqrt{3}$,-1),不妨取P(-$\sqrt{3}$,-1),
则$\overrightarrow{PA}$=($\sqrt{3}$,0),$\overrightarrow{PQ}$=(cosα+$\sqrt{3}$,sinα+1),
∴$\overrightarrow{PA}$•$\overrightarrow{PQ}$=$\sqrt{3}$(cosα+$\sqrt{3}$)=$\sqrt{3}$cosα+3;
又cosα∈[-1,1],
∴3-$\sqrt{3}$≤$\sqrt{3}$cosα+3≤3+$\sqrt{3}$,
即$\overrightarrow{PA}$$•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
故答案为:[3-$\sqrt{3}$,3+$\sqrt{3}$].
点评 本题考查了平面向量的数量积以及数形结合的数学思想,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-15,25) | B. | [-15,15] | C. | [0,25) | D. | [0,15] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
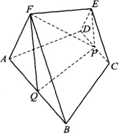 如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.
如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.
社区服务是综合实践活动课程的重要内容.上海市教育部门在全市高中学生中随机抽取200位学生参加社区服务的数据,按时间段[65,70),[70,75),[75,80),[80,85),[85,90)(单位:小时)进行统计,其频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com