
分析 建立平面直角坐标系,则A(0,0),B(0,1),C(2,0),M($\frac{1}{2}cosθ$,$\frac{1}{2}sinθ$),(0<θ<$\frac{π}{2}$),由已知可得$λ=\frac{1}{2}sinθ,2μ=\frac{1}{2}cosθ$,则λ+2μ=$\frac{1}{2}(sinθ+cosθ)=\frac{\sqrt{2}}{2}sin(θ+\frac{π}{4})$,即可求解.
解答 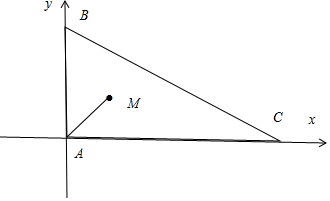 解:如图建立平面直角坐标系,则A(0,0),B(0,1),C(2,0)
解:如图建立平面直角坐标系,则A(0,0),B(0,1),C(2,0)
M($\frac{1}{2}cosθ$,$\frac{1}{2}sinθ$)(0<θ<$\frac{π}{2}$),
∵$\overrightarrow{AM}=λ\overrightarrow{AB}+μ\overrightarrow{AC}$,∴($(\frac{1}{2}cosθ,\frac{1}{2}sinθ)=λ(0,1)+μ(2,0)$.
∴$λ=\frac{1}{2}sinθ,2μ=\frac{1}{2}cosθ$,
则λ+2μ=$\frac{1}{2}(sinθ+cosθ)=\frac{\sqrt{2}}{2}sin(θ+\frac{π}{4})$,
∴当θ=$\frac{π}{4}$时,λ+2μ最大值为$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$
点评 本题考查向量的线性运算,平面向量的基本定理及其意义,建立坐标系,利用坐标运算,是一种常见的处理技巧,属于中档题.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:解答题
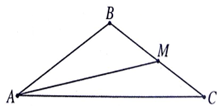 如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.
如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
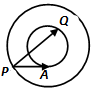 如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 愿意被外派 | 不愿意被外派 | 合计 | |
| 70后 | 20 | 20 | 40 |
| 80后 | 40 | 20 | 60 |
| 合计 | 60 | 40 | 100 |
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com