
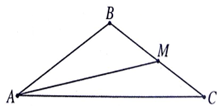
 如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.
如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.分析 (Ⅰ)由已知利用两角差的正切函数公式可求tanB的值,结合范围0<B<π,可求B的值.
(Ⅱ)由(Ⅰ)知B=$\frac{3π}{4}$,可得$β=B-α=\frac{3π}{4}-α$,利用三角函数恒等变换的应用化简可得$\sqrt{2}$sinα-sinβ=sin(α-$\frac{π}{4}$),结合范围$0<α<\frac{3π}{4}$,利用正弦函数的图象和性质可求其取值范围.
解答 解:(Ⅰ)$tanB=tan(∠AMC-∠BAM)=\frac{{-\frac{1}{2}-\frac{1}{3}}}{{1+(-\frac{1}{2})•\frac{1}{3}}}=-1$,
∵0<B<π,
∴$B=\frac{3π}{4}$.
(Ⅱ)由(Ⅰ)知B=$\frac{3π}{4}$,
∵α+β=B,∴$β=B-α=\frac{3π}{4}-α$,
∴$\sqrt{2}sinα-sinβ=\sqrt{2}sinα-sin(\frac{3π}{4}-α)$
=$\frac{{\sqrt{2}}}{2}sinα-\frac{{\sqrt{2}}}{2}cosα$=$sin(α-\frac{π}{4})$,
∵$0<α<\frac{3π}{4}$,
∴$-\frac{π}{4}<α-\frac{π}{4}<\frac{π}{2}$,
∴$-\frac{{\sqrt{2}}}{2}<sin(α-\frac{π}{4})<1$,
∴$\sqrt{2}sinα-sinβ$的取值范围是$(-\frac{{\sqrt{2}}}{2},1)$.
点评 本题主要考查了两角差的正切函数公式,三角函数恒等变换的应用,正弦函数的图象和性质在三角函数化简求值中的应用,考查了转化思想和数形结合思想的应用,属于基础题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
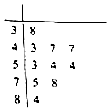 AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )
AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )| A. | 3 | B. | 4 | C. | 12 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,2) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
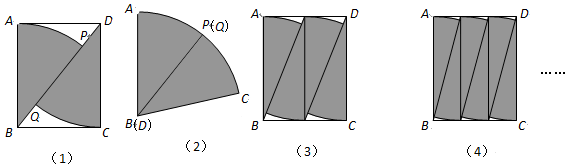
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | C. | 大于$\frac{π}{2}$ | D. | 大于1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com