
分析 (Ⅰ)利用绝对值不等式的几何意义直接证明:f(x)≥4;
(Ⅱ)利用(1)的结果,利用基本不等式转化求解即可.
解答 (Ⅰ)证明:$f(x)=|x-4m|+|x+\frac{1}{m}|≥|4m+\frac{1}{m}|=4|m|+|\frac{1}{m}|≥4$,
当且仅当$|m|=\frac{1}{2}$时取“=”号.
(Ⅱ)解:由题意知,k=4,即a+b=4,即$\frac{a}{4}+\frac{b}{4}=1$,
则$\frac{1}{a}+\frac{4}{b}=(\frac{1}{a}+\frac{4}{b})(\frac{a}{4}+\frac{b}{4})=\frac{5}{4}+\frac{b}{4a}+\frac{a}{b}≥\frac{5}{4}+1=\frac{9}{4}$,
当且仅当$a=\frac{4}{3}$,$b=\frac{8}{3}$时取“=”号.
点评 本题考查函数的最值的求法,基本不等式的应用,不等式的证明,考查计算能力.


科目:高中数学 来源: 题型:解答题
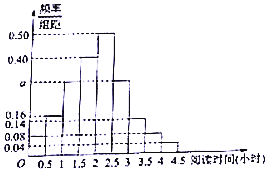 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
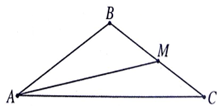 如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.
如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
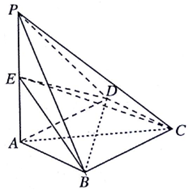 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,PA=AB=2,E为PA的中点,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
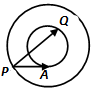 如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].
如图同心圆中,大、小圆的半径分别为2和1,点P在大圆上,PA与小圆相切于点A,Q为小圆上的点,则$\overrightarrow{PA}•\overrightarrow{PQ}$的取值范围是[3-$\sqrt{3}$,3+$\sqrt{3}$].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com