
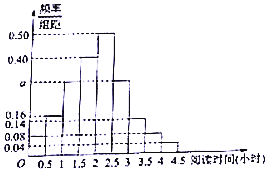
 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.分析 (Ⅰ)求出高一学生周末“阅读时间”在[0,0.5),[0.5,1),…,[4,4.5]的概率,即可求图中a的值;
(Ⅱ)确定2≤m<2.5,由0.50(m-2)=0.5-0.47,得m的值,即可估计该校高一学生周末“阅读时间”的中位数;
(Ⅲ)从全校高一年级随机抽取20名学生,“阅读时间”在[1,2.5]小时内的学生有X人,则X~B(20,0.6),恰好有k名学生的概率为P(X=k)=${C}_{20}^{k}•0.{6}^{k}•0.{4}^{20-k}$,其中k=0,1,2,…20.t=$\frac{P(X=k)}{P(X=k-1)}$=$\frac{3(21-k)}{2k}$,即可得出结论.
解答 解:(Ⅰ)由题意,高一学生周末“阅读时间”在[0,0.5),[0.5,1),…,[4,4.5]的概率分别为0.04,0.08,0.20.0.25.0.07,0.04.0.02,
由1-(0.04+0.08+0.20+0.25+0.07+0.04+0.02)=0.5a+0.5a,∴a=0.30;
(Ⅱ)设该校高一学生周末“阅读时间”的中位数为m小时,
因为前5组频率和为0.040.08+0.15+0.20+0.25=0.72>0.5,前4组频率和为0.47<0.5,
所以2≤m<2.5,
由0.50(m-2)=0.5-0.47,得m=2.06;
(Ⅲ)从全校高一年级随机抽取20名学生,“阅读时间”在[1,2.5]小时内的学生有X人,则X~B(20,0.6),恰好有k名学生的概率为P(X=k)=${C}_{20}^{k}•0.{6}^{k}•0.{4}^{20-k}$,其中k=0,1,2,…20.
t=$\frac{P(X=k)}{P(X=k-1)}$=$\frac{3(21-k)}{2k}$,
t>1,k<12.6,P(X=k-1)<P(X-k),
t<1,k>12.6,P(X=k-1)>P(X-k),
∴k=12,P(X=k)取最大.
点评 本题主要考查频率分步直方图,中位数,考查概率的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )
AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )| A. | 3 | B. | 4 | C. | 12 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
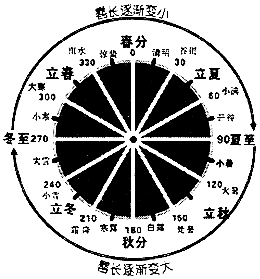 我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )
我国古代的天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气晷(guǐ)长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长的变化量相同,周而复始.若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长是( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 四尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
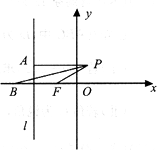 如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.
如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com