
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
分析 由$\sqrt{2}αcosB=\sqrt{2}c-b$,得$\sqrt{2}cosAsinB-sinB=0$,即cosA=$\frac{\sqrt{2}}{2}$,得A=$\frac{π}{4}$.
由$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=m\overrightarrow{AO}$,得$\frac{cosB}{snC}{\overrightarrow{AB}}^{2}+\frac{cosC}{sinB}\overrightarrow{AC}•\overrightarrow{AB}=m\overrightarrow{AO}•\overrightarrow{AB}$,
⇒$cosB+cosAcosC=\frac{1}{2}msinC$
则m=2×$\frac{cosB+cosAcosC}{sinC}$=2×$\frac{-cos(A+C)+cosAcosC}{sinC}$=2×$\frac{sinAsinC}{sinC}=2sinA$.
解答 解:∵$\sqrt{2}αcosB=\sqrt{2}c-b$,∴$\sqrt{2}sinAcosB=\sqrt{2}sin(A+B)-sinB$
⇒$\sqrt{2}sinAcosB=\sqrt{2}sinAcosB+\sqrt{2}cosAsinB-sinB\\;\\;\\;\$
⇒$\sqrt{2}cosAsinB-sinB=0$,∴cosA=$\frac{\sqrt{2}}{2}$,得A=$\frac{π}{4}$.
∵O是△ABC外接圆的圆心,∴$\overrightarrow{AO}•\overrightarrow{AB}=\frac{1}{2}{\overrightarrow{AB}}^{2}=\frac{1}{2}{c}^{2}$
由$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=m\overrightarrow{AO}$,得$\frac{cosB}{snC}{\overrightarrow{AB}}^{2}+\frac{cosC}{sinB}\overrightarrow{AC}•\overrightarrow{AB}=m\overrightarrow{AO}•\overrightarrow{AB}$,
⇒$\frac{cosB}{sinC}{c}^{2}+\frac{cosC}{sinB}bccosA=m×\frac{1}{2}{c}^{2}$⇒$\frac{cosB}{sinC}c+\frac{cosC}{sinB}bcosA=\frac{1}{2}mc$
⇒$cosB+cosAcosC=\frac{1}{2}msinC$
∴m=2×$\frac{cosB+cosAcosC}{sinC}$=2×$\frac{-cos(A+C)+cosAcosC}{sinC}$
=2×$\frac{sinAsinC}{sinC}=2sinA$=$\sqrt{2}$.
故选:C
点评 本题综合考查了三角形的外接圆的性质、向量的三角形法则、数量积运算、正弦定理、三角形的内角和定理、两角和的圆心公式等基础知识与基本技能,考查了数形结合的能力、推理能力、计算能力.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
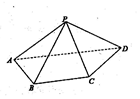 如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.
如图,已知四边形ABCD为直角梯形,∠DAB=∠ABC=90°,AB=1,AD=2BC=$\sqrt{2}$,若△PAD是以AD为底边的等腰直角三角形,且PA⊥CD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
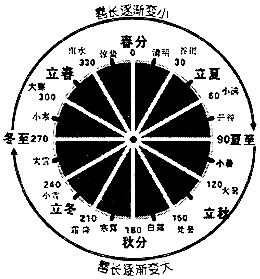 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
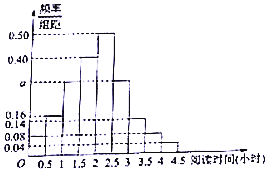 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com