
分析 由圆C:(x-a)2+(y-b)2=2,圆心C在曲线y=$\frac{1}{x}$(x∈[1,2])上,可得ab,利用弦长公式,可得结论.
解答 解:∵圆C:(x-a)2+(y-b)2=2,圆心C在曲线y=$\frac{1}{x}$(x∈[1,2])上,
∴ab=1,
圆心到直线的距离d=$\frac{|a+2b|}{\sqrt{5}}$=$\frac{|\frac{1}{b}+2b|}{\sqrt{5}}$,
∵a∈[1,2],∴b∈[$\frac{1}{2}$,1],
∴d∈[$\frac{2\sqrt{2}}{\sqrt{5}}$,$\frac{3}{\sqrt{5}}$],
∴直线l:x+2y=0被圆C所截得的长度的取值范围是[$\frac{2\sqrt{5}}{5}$,$\frac{2\sqrt{10}}{5}$]
故答案为1,[$\frac{2\sqrt{5}}{5}$,$\frac{2\sqrt{10}}{5}$].
点评 本题考查直线与圆位置关系的运用,考查弦长公式,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | $4\sqrt{3}π$ | C. | $\frac{8}{3}$π | D. | $\frac{4\sqrt{3}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
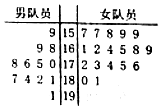 为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
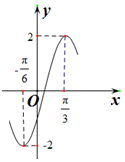 函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )
函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )| A. | $[\frac{π}{3},π]$和$[\frac{11π}{6},2π]$ | B. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{4π}{3},\frac{11π}{6}]$ | ||
| C. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{11π}{6},2π]$ | D. | $[\frac{π}{3},π]$和$[\frac{4π}{3},\frac{11π}{6}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
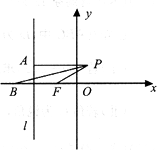 如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.
如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com