Question

4．已知点M（a，b）与点N（0，-1）在直线3x-4y+5=0的两侧，给出以下结论：
①3a-4b+5＞0；
②当a＞0时，a+b有最小值，无最大值；
③a²+b²＞1；
④当a＞0且a≠1时，$\frac{b+1}{a-1}$的取值范围是（-∞，-$\frac{9}{4}$）∪（$\frac{3}{4}$，+∞）．
正确的个数是（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 根据点M（a，b）与点N（1，0）在直线3x-4y+5=0的两侧，可以画出点M（a，b）所在的平面区域，进而结合二元一次不等式的几何意义，两点之间距离公式的几何意义，及两点之间连线斜率的几何意义，逐一分析四个命题得结论．

解答 解：∵点M（a，b）与点N（0，-1）在直线3x-4y+5=0的两侧，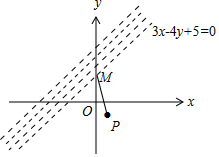
∴（3a-4b+5）（3×0+4+5）＜0，即3a-4b+5＜0，故①错误；
当a＞0时，a+b＞$\frac{5}{4}$，a+b即无最小值，也无最大值，故②错误；
设原点到直线3x-4y+5=0的距离为d，则d=$\frac{|10|}{\sqrt{{3}^{2}+（-4）^{2}}}=2$，则a²+b²＞4，故③错误；
当a＞0且a≠1时，$\frac{b+1}{a-1}$表示点M（a，b）与P（1，-1）连线的斜率．
∵当a=0，b=$\frac{5}{4}$时，$\frac{b+1}{a-1}$=$\frac{\frac{5}{4}+1}{-1}=-\frac{9}{4}$，又直线3x-4y+5=0的斜率为$\frac{3}{4}$，
故$\frac{b+1}{a-1}$的取值范围为（-∞，-$\frac{9}{4}$）∪（$\frac{3}{4}$，+∞），故④正确．
∴正确命题的个数是2个．
故选：B．

点评 本题考查的知识点是命题的真假判断与应用，线性规划的简单应用，考查数学转化思想方法，是中档题．