
分析 由函数y=Asin(ωx+φ)的图象变换可得f(x),由$\frac{ωπ}{12}$-$\frac{π}{8}$=$\frac{kπ}{2}$时,即ω=6k+$\frac{3}{2}$时f(x)为偶函数,从而可求实数ω的最小值.
解答 解:∵将函数f(x)=$|sin(ωx-\frac{π}{8})|(ω>0)$的图象向左平移$\frac{π}{12}$个单位后,所得图象对应的函数解析式为:
f(x)=|sin[ω(x+$\frac{π}{12}$)-$\frac{π}{8}$]|=|sin[ωx+($\frac{ωπ}{12}$-$\frac{π}{8}$)]|,
∵当 $\frac{ωπ}{12}$-$\frac{π}{8}$=$\frac{kπ}{2}$时,即ω=6k+$\frac{3}{2}$时,
f(x)=|sin(ωx+$\frac{kπ}{2}$)|=|-cos(ωx)|=|cos(ωx)|,f(x)为偶函数.
∵ω>0,
∴当k=0时,ω有最小值$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换,三角函数的图象与性质,属于基本知识的考查.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a∈R,函数f(x)是奇函数 | B. | ?a∈R,函数f(x)是偶函数 | ||
| C. | ?a>0,函数f(x)在(-∞,0)上是减函数 | D. | ?a>0,函数f(x)在(0,+∞)上是减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | $4\sqrt{3}π$ | C. | $\frac{8}{3}$π | D. | $\frac{4\sqrt{3}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
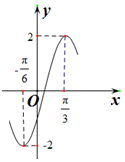 函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )
函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )| A. | $[\frac{π}{3},π]$和$[\frac{11π}{6},2π]$ | B. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{4π}{3},\frac{11π}{6}]$ | ||
| C. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{11π}{6},2π]$ | D. | $[\frac{π}{3},π]$和$[\frac{4π}{3},\frac{11π}{6}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com