
���� �������ۣ����ݶ��廯��Cxn�����Cx10�ı���ʽ�������ú����ĵ��������Cx10��ֵ��
��� �⣺��x��[$\frac{3}{2}$��2��ʱ��[x]=1����f��x��=C${\;}_{10}^{x}$=$\frac{10}{x}$��
��x��[$\frac{3}{2}$��2��ʱ��f��x���Ǽ���������f��x���ʣ�5��$\frac{20}{3}$����
��x��[2��3��ʱ��[x]=2����f��x��=C${\;}_{10}^{x}$=$\frac{90}{x��x-1��}$��
��x��[2��3��ʱ��f��x���Ǽ���������f��x���ʣ�15��45]��
�൱$x��[{\frac{3}{2}\;��\;3}��$ʱ������f��x��=C${\;}_{10}^{x}$��ֵ����$��{5\;��\;\frac{20}{3}}]�ȣ�{15\;��\;45}]$��
�ʴ�Ϊ��$��{5\;��\;\frac{20}{3}}]�ȣ�{15\;��\;45}]$��
���� ���⿼�����¶���ĺ�����Ӧ�����⣬Ҳ������������ijһ�����ϵ���ֵ���⣬����ʱӦ������û���֪ʶ���Ա������⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
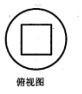 ��һ�������У��ڳ�һ��������ij����壬�ں���ĸ���ͼ��ͼ������������ͼ��ȷ���ǣ�������
��һ�������У��ڳ�һ��������ij����壬�ں���ĸ���ͼ��ͼ������������ͼ��ȷ���ǣ�������| A�� | 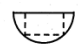 | B�� | 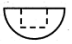 | C�� |  | D�� | 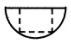 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com