练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
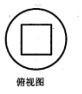
    18．在一个半球中，挖出一个体积最大的长方体，挖后几何体的俯视图如图，则下列正视图正确的是（　　）
    A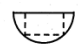．B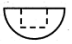．C．D．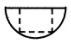

    分析 由题意，挖出一个体积最大的长方体，由俯视图，可知正视图投影线不能到底部，即可得答案．

    解答 解：由题意，挖出一个体积最大的长方体，看成是整球里边接一个正方体，砍掉一半，即半球里的最大长方体．其长与宽相等，其高是长的一半!当棱长都是半球内的半径时，其体积最大．
    显然，高只能是半径的一半，投影线不能到底部．
    由俯视图，可知正视图投影线不能到底部，排除A，D选项．
    B选项视图可知，挖出是一个正方体，∴B不对．
    故而C满足题意．
    故选C

    点评 本题考查了三视图与空间几何体的投影关系，考虑空间想象能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    8．设x∈R，用[x]表示不超过x的最大整数（如[2.32]=2，[-4.76]=-5），对于给定的n∈N*，定义C${\;}_{n}^{x}$=$\frac{n（n-1）…（n-[x]+1）}{x（x-1）…（x-[x]+1）}$，其中x∈[1，+∞），则当$x∈[{\frac{3}{2}\;，\;3}）$时，函数f（x）=C${\;}_{10}^{x}$的值域是$（{5\;，\;\frac{20}{3}}]∪（{15\;，\;45}]$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

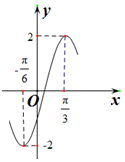    6．函数y=Asin（ωx+ϕ）$（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，则其在区间$[\frac{π}{3}，2π]$上的单调递减区间是（　　）
    A．$[\frac{π}{3}，π]$和$[\frac{11π}{6}，2π]$B．$[\frac{π}{3}，\frac{5π}{6}]$和$[\frac{4π}{3}，\frac{11π}{6}]$
    C．$[\frac{π}{3}，\frac{5π}{6}]$和$[\frac{11π}{6}，2π]$D．$[\frac{π}{3}，π]$和$[\frac{4π}{3}，\frac{11π}{6}]$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知某椎体的正视图和侧视图如图，则该锥体的俯视图不可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．在△ABC中，内角A，B，C的对边分别为a，b，c，O是△ABC外接圆的圆心，若$\sqrt{2}αcosB=\sqrt{2}c-b$，且$\frac{cosB}{sinC}\overrightarrow{AB}+\frac{cosC}{sinB}\overrightarrow{AC}=m\overrightarrow{AO}$，则m的值是（　　）
    A．$\frac{{\sqrt{2}}}{4}$B．$\frac{{\sqrt{2}}}{2}$C．$\sqrt{2}$D．$2\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．设f（x）=$\frac{{|{ax+1}|-|{2x-1}|}}{|x|}$．
    （1）当a=2时，求不等式f（x）＞1的解集；
    （2）若对任意a∈（0，1），x∈{x|x≠0}，不等式f（x）≤b恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

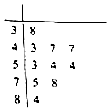    7．AQI（Air　Quality　Index，空气质量指数）是报告每日空气质量的参数，描述了空气清洁或者污染的程度．AQI共分六级，从一级优（0～50），二级良（51～100，），三级轻度污染（101～150），四级重度污染（151～200），直至无极重度污染（201～300），六级严重污染（大于300）．下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图，利用该样本估计昆明市2018年4月份质量优的天数（按这个月共30天计算）为（　　）
    A．3B．4C．12D．21

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=4sinxcos（x-$\frac{π}{6}$）+1．
    （Ⅰ）求函数f（x）的最小正周期；
    （Ⅱ）求函数f（x）在区间[-$\frac{π}{6}$，$\frac{π}{4}$]上的最大值．

    查看答案和解析>>

    同步练习册答案