
分析 (1)通过讨论x的范围,求出不等式的解集即可;
(2)问题转化为b≥f(x)max=a+2,求出b的范围即可.
解答 解:(1)当a=2时,由f(x)>1得,|2x+1|-|2x-1|>|x|,
x>$\frac{1}{2}$时,2x+1-2x+1>x,解得:x<2;
0≤x≤$\frac{1}{2}$时,2x+1+2x-1>x,解得:x>0,
-$\frac{1}{2}$<x<0时,2x+1+2x-1>-x,解得:x>0(舍),
x≤-$\frac{1}{2}$时,-2x-1+2x-1>-x,解得:x>2(舍),
所以不等式f(x)≥1的解集为(0,2);
(2)不等式f(x)≤b得:
b≥f(x)max,$\frac{|ax+1|-|2x-1|}{|x|}≤\frac{|ax+2x|}{|x|}=|a+2|$,
∴b≥f(x)max=a+2,
又因为对任意的a∈(0,1)恒成立,
所以b≥3.
点评 本题考查了解绝对值不等式问题,考查函数恒成立问题以及分类讨论思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
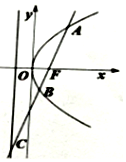 如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$.
如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
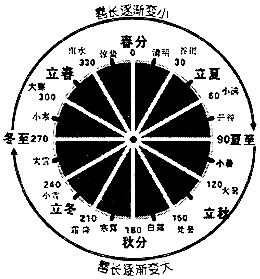 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com