
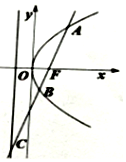
 如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$.
如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$. 分析 分别过A,F,B作准线的垂线,垂足分别为A1,D,B1,利用相似三角形计算BB1,AA1即可得出AB=AA1+BB1.
解答  解:分别过A,F,B作准线的垂线,垂足分别为A1,D,B1,
解:分别过A,F,B作准线的垂线,垂足分别为A1,D,B1,
则DF=p=2,由抛物线的定义可知BF=BB1,AF=AA1,
∵$\overrightarrow{FC}$=4$\overrightarrow{FB}$,∴$\frac{DF}{B{B}_{1}}=\frac{FC}{BC}=\frac{4}{3}$,∴BF=BB1=$\frac{3}{2}$.
∴CF=4FB=6,
∴cos∠DFC=$\frac{DF}{CF}=\frac{1}{3}$,
∴cos∠A1AC=$\frac{A{A}_{1}}{AC}$=$\frac{AF}{AF+6}$=$\frac{1}{3}$,解得AF=3,
∴AB=AF+BF=3+$\frac{3}{2}$=$\frac{9}{2}$.
故答案为:$\frac{9}{2}$.
点评 本题考查了抛物线的性质,属于中档题.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
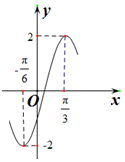 函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )
函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )| A. | $[\frac{π}{3},π]$和$[\frac{11π}{6},2π]$ | B. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{4π}{3},\frac{11π}{6}]$ | ||
| C. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{11π}{6},2π]$ | D. | $[\frac{π}{3},π]$和$[\frac{4π}{3},\frac{11π}{6}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N=M | B. | M∪N=R | C. | M∩∁RN=φ | D. | ∁RM∪N=R |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com