
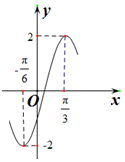
 函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )
函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示,则其在区间$[\frac{π}{3},2π]$上的单调递减区间是( )| A. | $[\frac{π}{3},π]$和$[\frac{11π}{6},2π]$ | B. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{4π}{3},\frac{11π}{6}]$ | ||
| C. | $[\frac{π}{3},\frac{5π}{6}]$和$[\frac{11π}{6},2π]$ | D. | $[\frac{π}{3},π]$和$[\frac{4π}{3},\frac{11π}{6}]$ |
分析 由函数y=Asin(ωx+ϕ)的图象可得A=2,$\frac{1}{2}$T=$\frac{π}{3}$-(-$\frac{π}{6}$)=$\frac{π}{2}$,由T=π=$\frac{2π}{ω}$,可解得ω=2;再由“五点作图法”解得:φ=-$\frac{π}{6}$,从而可得y=2sin(2x-$\frac{π}{6}$),利用正弦函数的单调性,解不等式2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$(k∈Z)后,再对k赋值0与1,即可求得函数y=2sin(2x-$\frac{π}{6}$)在区间$[\frac{π}{3},2π]$上的单调递减区间.
解答 解:由函数y=Asin(ωx+ϕ)$(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象可知,
A=2,$\frac{1}{2}$T=$\frac{π}{3}$-(-$\frac{π}{6}$)=$\frac{π}{2}$,故T=π=$\frac{2π}{ω}$,解得ω=2;
由“五点作图法”得:2×$\frac{π}{3}$+φ=$\frac{π}{2}$,解得:φ=-$\frac{π}{6}$.
所以,y=2sin(2x-$\frac{π}{6}$).
由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$(k∈Z)得:
kπ+$\frac{π}{3}$≤x≤kπ+$\frac{5π}{6}$(k∈Z).
当k=0时,$\frac{π}{3}$≤x≤$\frac{5π}{6}$;
当k=1时,$\frac{4π}{3}$≤x≤$\frac{11π}{6}$;
综上所述,函数y=2sin(2x-$\frac{π}{6}$)在区间$[\frac{π}{3},2π]$上的单调递减区间是[$\frac{π}{3}$,$\frac{5π}{6}$]和[$\frac{4π}{3}$,$\frac{11π}{6}$].
故选:B.
点评 本题考查本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,求得ω与φ是关键,考查正弦函数的单调性,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
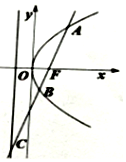 如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$.
如图,过抛物线y2=4x的焦点F作直线与抛物线及其准线分别交于A,B,C三点,若$\overrightarrow{FC}$=4$\overrightarrow{FB}$,则$|{\overrightarrow{AB}}|$=$\frac{9}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
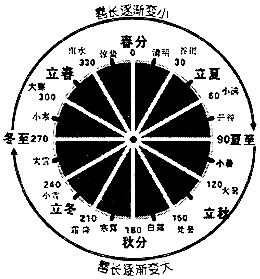 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com