
分析 (I)通过抛物线方程可知c=1,利用P($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$)及椭圆定义可知=2,进而可得结论;
(II)通过分析确定直线l1的斜率存在且不为0,通过设A(x1,y1),B(x2,y2),直线l1:y=k(x-1),直线l2:y=-$\frac{1}{k}$(x-1),利用两点间距离公式及|CD|=4|AB|可求出k的值,进而可得结论.
解答 解:(I)由已知,F(1,0),即c=1,
由|PF|=$\frac{5}{3}$且点P在第一象限内,可知P($\frac{2}{3}$,$\frac{2\sqrt{6}}{3}$),
由椭圆定义可知2a=$\sqrt{(\frac{2}{3}-1)^{2}+(\frac{2\sqrt{6}}{3}-0)^{2}}$+$\sqrt{(\frac{2}{3}+1)^{2}+(\frac{2\sqrt{6}}{3}-0)^{2}}$=4,即a=2,
∴b2=a2-c2=3,∴椭圆M的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(II)由题可知,直线l1的斜率必存在.
①当直线l1的斜率为0时,则直线l2的斜率不存在,此时|CD|=4,|AB|=4,不满足题意;
②当直线l1的斜率存在且不为0时,设A(x1,y1),B(x2,y2),
设直线l1:y=k(x-1),则直线l2:y=-$\frac{1}{k}$(x-1),
联立直线l1与椭圆M的方程,消去y得:(4k2+3)x2-8k2x+4k2-12=0,
从而|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{(8{k}^{2})^{2}-4(4{k}^{2}+3)(4{k}^{2}-12)}}{4{k}^{2}+3}$=$\frac{12({k}^{2}+1)}{4{k}^{2}+3}$,
联立直线l2与抛物线E的方程,消去y得:$\frac{1}{{k}^{2}}$x2-2($\frac{1}{{k}^{2}}$+2)x+$\frac{1}{{k}^{2}}$=0,
从而|CD|=x1+x2+2=$\frac{2(\frac{1}{{k}^{2}}+2)}{\frac{1}{{k}^{2}}}$+2=4(k2+1),
由|CD|=4|AB|可知$\frac{12({k}^{2}+1)}{4{k}^{2}+3}$=k2+1,解得:k=±$\frac{3}{2}$,
所以直线l1的方程为:3x±2y-3.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
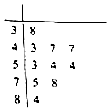 AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )
AQI(Air Quality Index,空气质量指数)是报告每日空气质量的参数,描述了空气清洁或者污染的程度.AQI共分六级,从一级优(0~50),二级良(51~100,),三级轻度污染(101~150),四级重度污染(151~200),直至无极重度污染(201~300),六级严重污染(大于300).下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图,利用该样本估计昆明市2018年4月份质量优的天数(按这个月共30天计算)为( )| A. | 3 | B. | 4 | C. | 12 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤3} | B. | {x|1<x<2} | C. | {x|0≤x≤1} | D. | {x|2<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∩N=M | B. | M∪N=R | C. | M∩∁RN=φ | D. | ∁RM∪N=R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,2) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com