练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知随机变量X～N（1，σ2），若P（X＞0）=0.8，则P（X≥2）=0.2．

    分析 随机变量ξ服从正态分布N（1，σ2），得到曲线关于x=1对称，根据P（X≥2）=P（X≤0）=1-P（X＞0）得到结果．

    解答 解：随机变量ξ服从正态分布N（1，σ2），
    ∴曲线关于x=1对称，
    ∴P（X≥2）=P（X≤0）=1-P（X＞0）=0.2
    故答案为：0.2．

    点评 本题主要考查正态分布曲线的特点及曲线所表示的意义、函数图象对称性的应用等基础知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    10．设f（x）=$\frac{{|{ax+1}|-|{2x-1}|}}{|x|}$．
    （1）当a=2时，求不等式f（x）＞1的解集；
    （2）若对任意a∈（0，1），x∈{x|x≠0}，不等式f（x）≤b恒成立，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

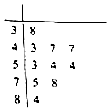    7．AQI（Air　Quality　Index，空气质量指数）是报告每日空气质量的参数，描述了空气清洁或者污染的程度．AQI共分六级，从一级优（0～50），二级良（51～100，），三级轻度污染（101～150），四级重度污染（151～200），直至无极重度污染（201～300），六级严重污染（大于300）．下面是昆明市2017年4月份随机抽取的10天的AQI茎叶图，利用该样本估计昆明市2018年4月份质量优的天数（按这个月共30天计算）为（　　）
    A．3B．4C．12D．21

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．已知集合M={x|1＜x≤3}，若N={x|0≤x＜2}，则M∪N=（　　）
    A．{x|0≤x≤3}B．{x|1＜x＜2}C．{x|0≤x≤1}D．{x|2＜x≤3}

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

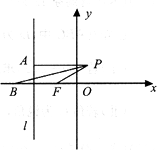    4．如图，在平面直角坐标系中，点F（-1，0），过直线l：x=-2右侧的动点P作PA⊥l于点A，∠APF的平分线交x轴于点B，|PA|=$\sqrt{2}$|BF|．
    （1）求动点P的轨迹C的方程；
    （2）过点F的直线q交曲线C于M，N，试问：x轴正半轴上是否存在点E，直线EM，EN分别交直线l于R，S两点，使∠RFS为直角？若存在，求出点E的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．若集合M={x|x2-x＜0}，N={y|y=ax（a＞0，a≠1）}，R表示实数集，则下列选项错误的是（　　）
    A．M∩N=MB．M∪N=RC．M∩∁RN=φD．∁RM∪N=R

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=4sinxcos（x-$\frac{π}{6}$）+1．
    （Ⅰ）求函数f（x）的最小正周期；
    （Ⅱ）求函数f（x）在区间[-$\frac{π}{6}$，$\frac{π}{4}$]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=$\frac{e^x}{x}$．
    （Ⅰ）求曲线y=f（x）在点P（2，$\frac{e^2}{2}$）处的切线方程；
    （Ⅱ）证明：f（x）＞2（x-lnx）．

    查看答案和解析>>

    同步练习册答案