
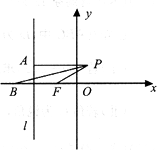
 如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.
如图,在平面直角坐标系中,点F(-1,0),过直线l:x=-2右侧的动点P作PA⊥l于点A,∠APF的平分线交x轴于点B,|PA|=$\sqrt{2}$|BF|.分析 (1)设P(x,y),由平面几何知识得$\frac{\sqrt{(x+1)^{2}+{y}^{2}}}{|x+2|}$=$\frac{\sqrt{2}}{2}$,由此能求出动点P的轨迹C的方程.
(2)假设满足条件的点E(n,0)(n>0)存在,设直线q的方程为x=my-1,联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=2}\\{x=my-1}\end{array}\right.$,得:(m2+2)y2-2my-1=0,由此利用韦达定理、直线方程、椭圆性质,结合已知条件能求出满足条件的点E存在,其坐标为($\sqrt{2}$,0).
解答 解:(1)设P(x,y),由平面几何知识得:
$\frac{|PF|}{|PA|}$=$\frac{\sqrt{2}}{2}$,即$\frac{\sqrt{(x+1)^{2}+{y}^{2}}}{|x+2|}$=$\frac{\sqrt{2}}{2}$,
化简,得:x2+2y2=2,
∴动点P的轨迹C的方程为x2+2y2=2(x$≠\sqrt{2}$).
(2)假设满足条件的点E(n,0)(n>0)存在,
设直线q的方程为x=my-1,
M(x1,y1),N(x2,y2),R(-2,y3),S(-2,y4),
联立$\left\{\begin{array}{l}{{x}^{2}+2{y}^{2}=2}\\{x=my-1}\end{array}\right.$,得:(m2+2)y2-2my-1=0,
y1+y2=$\frac{2m}{{m}^{2}+2}$,y1y2=-$\frac{1}{{m}^{2}+2}$,
${x}_{1}{x}_{2}=(m{y}_{1}-1)(m{y}_{2}-1)={m}^{2}{y}_{1}{y}_{2}-m({y}_{1}+{y}_{2})+1$
=-$\frac{{m}^{2}}{{m}^{2}+2}-\frac{2{m}^{2}}{{m}^{2}+2}$+1=$\frac{2-2{m}^{2}}{{m}^{2}+2}$,
${x}_{1}+{x}_{2}=m({y}_{1}+{y}_{2})-2=\frac{2{m}^{2}}{{m}^{2}+2}$=-$\frac{4}{{m}^{2}+2}$,
由条件知$\frac{{y}_{1}}{{x}_{1}-n}$=$\frac{{y}_{3}}{-2-n}$,y3=-$\frac{(2+n){y}_{1}}{{x}_{1}-n}$,
同理${y}_{4}=-\frac{(2+n){y}_{2}}{{x}_{2}-n}$,
${k}_{RF}=\frac{{y}_{3}}{-2+1}$=-y3,kSF=-y4,
由于∠RFS为直角,∴y3y4=-1,即(2+n2)y1y2=-[x1x2+n(x1+x2)+n2],
(2+n)2$\frac{1}{{m}^{2}+2}$=$\frac{2-2{m}^{2}}{{m}^{2}+2}$+$\frac{4n}{{m}^{2}+2}$+n2,
∴(n2-2)(m2+1)=0,解得n=$\sqrt{2}$,
∴满足条件的点E存在,其坐标为($\sqrt{2}$,0).
点评 本题考查点的轨迹方程的求法,考查韦达定理、直线方程、椭圆性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、方程与函数思想、数形结合思想,是中档题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
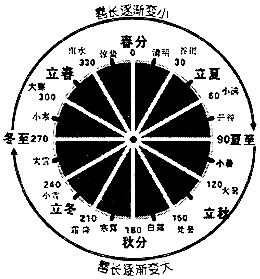 《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )
《周髀算经》是中国古代的天文学和数学著作.其中一个问题大意为:一年有二十四个节气,每个节气晷长损益相同(即太阳照射物体影子的长度增加和减少大小相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:一丈等于十尺,一尺等于十寸),则夏至之后的那个节气(小暑)晷长为( )| A. | 五寸 | B. | 二尺五寸 | C. | 三尺五寸 | D. | 一丈二尺五寸 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
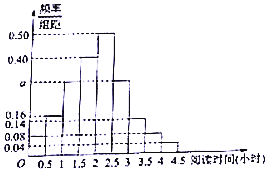 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4i | B. | -4i | C. | 2 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(3,+∞) | B. | {x|x>3,x∈N} | C. | {4,8} | D. | [4,8] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com