
分析 (Ⅰ)通过导函数求解切线的斜率,得到切点坐标,然后求解切线方程.
(Ⅱ)设函数$g(x)=f(x)-2(x-lnx)=\frac{e^x}{x}-2x+2lnx$,$g'(x)=\frac{{({e^x}-2x)(x-1)}}{x^2}$,x∈(0,+∞),
设h(x)=ex-2x,x∈(0,+∞),求出导函数,通过导函数的符号,求解g(x)min=g(1)=e-2>0,从而证明结果.
解答 解:(Ⅰ)∵$f(x)=\frac{e^x}{x}$,∴$f'(x)=\frac{{{e^x}(x-1)}}{x^2}$,$f'(2)=\frac{e^2}{4}$,又切点为$(2,\frac{e^2}{2})$,
所以切线方程为$y-\frac{e^2}{2}=\frac{e^2}{4}(x-2)$,即e2x-4y=0.
(Ⅱ)证明:设函数$g(x)=f(x)-2(x-lnx)=\frac{e^x}{x}-2x+2lnx$,$g'(x)=\frac{{({e^x}-2x)(x-1)}}{x^2}$,x∈(0,+∞),
设h(x)=ex-2x,x∈(0,+∞),则h'(x)=ex-2,令h'(x)=0,则x=ln2,
所以x∈(0,ln2),h'(x)<0;x∈(ln2,+∞),h'(x)>0.
则h(x)≥h(ln2)=2-2ln2>0,
令$g'(x)=\frac{{({e^x}-2x)(x-1)}}{x^2}=0$,可得x=1,
所以x∈(0,1),g'(x)<0;x∈(1,+∞),g'(x)>0;
则g(x)min=g(1)=e-2>0,从而有当x∈(0,+∞),f(x)>2(x-lnx).
点评 本题考查函数与导数的应用,函数的最值,构造法的应用,考查转化思想以及计算能力.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
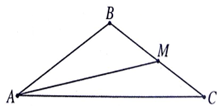 如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.
如图,在△ABC中,M是边BC上的点,且tan∠BAM=$\frac{1}{3}$,tan∠AMC=-$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com