
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 ①根据回归直线的定义判断即可;
②根据概念判断;
③存在命题的否定是把存在改为任意,再否定结论;
④得出p,q至少有一个为真,得出?p,?q则至少一个为假,得出结论.
解答 解:①回归直线$\widehaty=b\widehatx+a$恒过样本中心点$(\overline x,\overline y)$,由回归直线方程定义可知,正确;
②“x=6”能推出“x2-5x-6=0”,反之不一定,故应是充分不必要条件,故错误;
③“?x0∈R,使得x02+2x0+3<0”的否定是对?x∈R,均有x2+2x+3≥0,故错误;
④“命题p∨q”为真命题,则p,q至少有一个为真,则?p,?q则至少一个为假,故“命题?p∧?q”也是假命题,故错误.
故选B.
点评 本题考查了回归直线方程,充要条件,命题的否定,复合命题的概念.属于基础题型,应熟练掌握.


科目:高中数学 来源: 题型:选择题
| A. | {x|0≤x≤3} | B. | {x|1<x<2} | C. | {x|0≤x≤1} | D. | {x|2<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (-1,2) | C. | (0,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
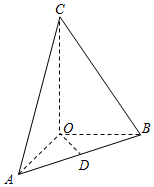 在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.
在三棱锥C-ABO中,OA、OB、OC所在直线两两垂直,且OA=OB,CA与平面AOB所成角为60°,D是AB中点,三棱锥C-ABO的体积是$\frac{{\sqrt{3}}}{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | ±1 | C. | 1或2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com