
分析 将直线$\left\{\begin{array}{l}x=t\\ y=6-2t\end{array}\right.$(t为参数)和曲线C:$\left\{\begin{array}{l}x=1+\sqrt{5}cosθ\\ y=-2+\sqrt{5}sinθ\end{array}\right.$(θ为参数)化为普通方程,利用圆心到直线的距离d减去半径r,可得|PQ|的最小值.
解答 解:由题意,曲线C:$\left\{\begin{array}{l}x=1+\sqrt{5}cosθ\\ y=-2+\sqrt{5}sinθ\end{array}\right.$,消去参数θ:
可得曲线C的普通方程为:(x-1)2+(y+2)2=5.
直线$\left\{\begin{array}{l}x=t\\ y=6-2t\end{array}\right.$(t为参数),消去参数t,可得直线的普通方程为:2x+y-6=0.
由曲线C的普通方程为:(x-1)2+(y+2)2=5.可知圆心为(1,-2),半径r=$\sqrt{5}$.
那么:圆心到直线的距离d=$\frac{|2×1-2-6|}{\sqrt{5}}$=$\frac{6\sqrt{5}}{5}$
可得|PQ|的最小值为:d-r=$\frac{6\sqrt{5}}{5}-\sqrt{5}$=$\frac{{\sqrt{5}}}{5}$;
故答案为:$\frac{\sqrt{5}}{5}$
点评 本题主要考查了参数方程化为普通方程,以及利用平面几何知识解决最值问题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
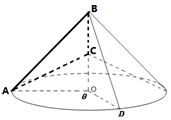 如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.
如图,等腰Rt△AOB,OA=OB=2,点C是OB的中点,△AOB绕BO所在的边逆时针旋转一周.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | $4\sqrt{3}π$ | C. | $\frac{8}{3}$π | D. | $\frac{4\sqrt{3}}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
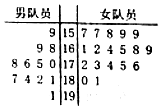 为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com