
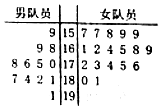
 为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.
为了检验训练情况,武警某支队于近期举办了一场展示活动,其中男队员12人,女队员18人,测试结果如茎叶图所示(单位:分).若成绩不低于175分者授予“优秀警员”称号,其他队员则给予“优秀陪练员”称号.分析 (1)根据茎叶图,有“优秀警员”12人,“优秀陪练员”18人.用分层抽样的方法,与古典概率计算公式即可得出.
(2)依题意,ξ的取值为0,1,2,3.利于古典概率计算公式即可得出.
解答 解:(1)根据茎叶图,有“优秀警员”12人,“优秀陪练员”18人
用分层抽样的方法,每个人被抽中的概率是$\frac{10}{30}=\frac{1}{3}$
所以选中的“优秀警员”有4人,“优秀陪练员”有6人.
用事件A表示“至少有1名“优秀警员”被选中”,
则$P(A)=1\frac{C_6^4}{{C_{10}^4}}$=$1-\frac{15}{210}=\frac{13}{14}$.
因此,至少有1人是“优秀警员”的概率是$\frac{13}{14}$
(2)依题意,ξ的取值为0,1,2,3.$p(ξ=0)=\frac{C_8^3}{{C_{12}^3}}=\frac{14}{55}$,$p(ξ=1)=\frac{C_4^1C_8^2}{{C_{12}^3}}=\frac{28}{55}$,$p(ξ=2)=\frac{C_4^2C_8^1}{{C_{12}^3}}=\frac{12}{55}$,$p(ξ=3)=\frac{C_4^3}{{C_{12}^3}}=\frac{1}{55}$,
因此,ξ的分布列如下:
| ξ | 0 | 1 | 2 | 3 |
| p | $\frac{14}{55}$ | $\frac{28}{55}$ | $\frac{12}{55}$ | $\frac{1}{55}$ |
点评 本题考查了茎叶图、分层抽样、古典概率计算公式、随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
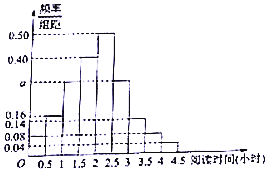 某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.
某校为了解高一学生周末的“阅读时间”,从高一年级中随机调查了100名学生进行调查,获得了每人的周末“阅读时间”(单位:小时),按图[0.0.5),[0.5,1),…,[4,4.5]分9组,制成样本的频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com