
| A. | 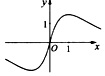 | B. | 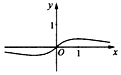 | C. | 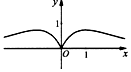 | D. | 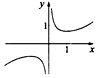 |
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:选择题
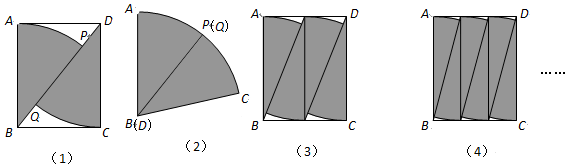
| A. | 小于$\frac{π}{2}$ | B. | 等于$\frac{π}{2}$ | C. | 大于$\frac{π}{2}$ | D. | 大于1.6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-15,25) | B. | [-15,15] | C. | [0,25) | D. | [0,15] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<3} | B. | {x|x>0} | C. | {x|1<x<3} | D. | {x|0<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
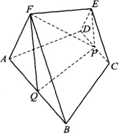 如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.
如图,在五面体ABCDEF中,面CDE和面ABF都为等边三角形,面ABCD是等腰梯形,点P、Q分别是CD、AB的中点,FQ∥EP,PF=PQ,AB=2CD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 月收入(单位:百元) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 25 | 100 | 150 | 155 | 50 | 20 |
| 赞成人数 | 10 | 70 | 120 | 150 | 35 | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
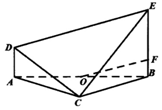 如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.
如图,在以A、B、C、D、E为顶点的五面体中,AD⊥平面ABC,AD∥BE,AC⊥CB,AB=2BE=4AD=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{121}{2}$,81] | B. | [$\frac{121}{2}$,73] | C. | [65,73] | D. | [65,81] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com