
| �������루��λ����Ԫ�� | [10��20�� | [20��30�� | [30��40�� | [40��50�� | [50��60�� | [60��70�� |
| ��Ƶ�� | ��25 | ��100 | ��150 | ��155 | ��50 | 20 |
| �������� | ��10 | ��70 | ��120 | ��150 | ��35 | ��15 |
���� ��1����20��������ѡȡ3�ˣ�����${C}_{20}^{3}$��ȡ�����ֱ����ǡ��2�˳���̬�ȵĸ��ʺ�ǡ��3�˳���̬�ȵĸ��ʣ��ɴ����û����¼����ʼ��㹫ʽ�����3��������2�˶ԶԸô�ʩ����̬�ȵĸ��ʣ�
��2����������Ը������߳���̬�ȵĸ���Ϊp=$\frac{4}{5}$��X�Ŀ���ȡֵΪ0��1��2��3����X��B��3��$\frac{4}{5}$�����ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����20��������ѡȡ3�ˣ�����${C}_{20}^{3}$��ȡ��������${C}_{20}^{3}$��ȡ���Ŀ�������ͬ��
ǡ��2�˳���̬�ȵĸ���p1=$\frac{{C}_{15}^{2}{C}_{5}^{1}}{{C}_{20}^{3}}$=$\frac{35}{76}$��
ǡ��3�˳���̬�ȵĸ���P2=$\frac{{C}_{15}^{3}{C}_{5}^{0}}{{C}_{20}^{3}}$=$\frac{91}{228}$��
��3��������2�˶ԶԸô�ʩ����̬�ȵĸ���p=p1+p2=$\frac{35}{76}+\frac{91}{228}$=$\frac{49}{57}$��
��2����500���г��ɵ�Ƶ��p3=$\frac{10+70+120+150+35+15}{500}$=$\frac{4}{5}$��
��ɹ�������Ը������߳���̬�ȵĸ���Ϊp=$\frac{4}{5}$��
X�Ŀ���ȡֵΪ0��1��2��3����X��B��3��$\frac{4}{5}$����
P��X=0��=${C}_{3}^{0}��\frac{4}{5}��^{0}��\frac{1}{5}��^{3}$=$\frac{1}{125}$��
P��X=1��=${C}_{3}^{1}��\frac{4}{5}����\frac{1}{5}��^{2}$=$\frac{12}{125}$��
P��X=2��=${C}_{3}^{2}��\frac{4}{5}��^{2}��\frac{1}{5}��$=$\frac{48}{125}$��
P��X=3��=${C}_{3}^{3}��\frac{4}{5}��^{3}��\frac{1}{5}��^{0}$=$\frac{64}{125}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{125}$ | $\frac{12}{125}$ | $\frac{48}{125}$ | $\frac{64}{125}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��С���ѧ������������������֤����������������������黯����ת��˼�롢���ν��˼�룬���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 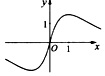 | B�� | 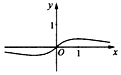 | C�� | 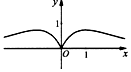 | D�� | 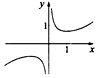 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | 2 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| Ը�ⱻ���� | ��Ը�ⱻ���� | �ϼ� | |
| 70�� | 20 | 20 | 40 |
| 80�� | 40 | 20 | 60 |
| �ϼ� | 60 | 40 | 100 |
| P��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com